Tìm tất cả các giá trị của tham số m để hàm số y = log2020 (mx - m + 2) xác định
Câu hỏi:
Tìm tất cả các giá trị của tham số m để hàm số \[y = {\log _{2020}}(mx - m + 2)\]xác định trên \[[1; + \infty )\].
Trả lời:
Điều kiện xác định: mx – m + 2 > 0 ⇔ m(x − 1) > −2
Để hàm số xác định trên [1;+∞) thì m(x − 1) > −2 ∀x ≥ 1 (∗)
+) x = 1Û 0m > −2 đúng với mọi m
+) x > 1\[ \Leftrightarrow m > \frac{{ - 2}}{{x - 1}},\,\,\forall x > 1\,\,\](**)
Xét hàm số \[f(x) = \frac{{ - 2}}{{x - 1}},\,\,\forall x > 1\]
\[f'(x) = \frac{2}{{{{(x - 1)}^2}}} > 0,\,\,\forall x \in (1; + \infty )\,\,\]
Bảng biến thiên:
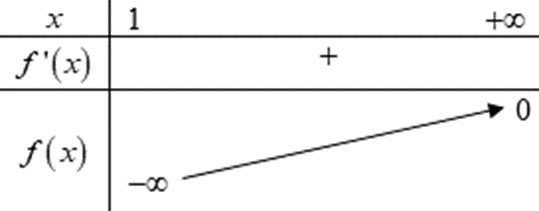
Dựa vào bảng biến thiên:
Þ m ≥ 0
Vậy để hàm số \[y = {\log _{2020}}(mx - m + 2)\] xác định trên \[[1; + \infty )\] thì m ≥ 0.


