Tìm tất cả các giá trị của tham số m để phương trình 4(log2 căn bậc hai x)^2
Câu hỏi:
Tìm tất cả các giá trị của tham số m để phương trình \(4{\left( {{{\log }_2}\sqrt x } \right)^2} - {\log _{\frac{1}{2}}}x\) + m = 0 có nghiệm thuộc khoảng (0; 1).
Trả lời:
ĐK: x > 0.
Ta có: \(4{\left( {{{\log }_2}\sqrt x } \right)^2} - {\log _{\frac{1}{2}}}x + m = 0\)
⇔ \(4{\left( {\frac{1}{2}{{\log }_2}x} \right)^2} - {\log _{{2^{ - 1}}}}x + m = 0\)
⇔ \({\left( {{{\log }_2}x} \right)^2} + {\log _2}x + m = 0\)
Đặt \(t = {\log _2}x\) với x ∈ (0; 1) ⇒ t < 0
Khi đó: t2 + t + m = 0 ⇔ \( - m = {t^2} + t = f\left( t \right)\).
Xét hàm số \(f\left( t \right) = {t^2} + t\) trên (-∞; 0), có \(f'\left( t \right) = 2t + 1 = 0\) ⇔ \(t = - \frac{1}{2}\).
Bảng biến thiên:
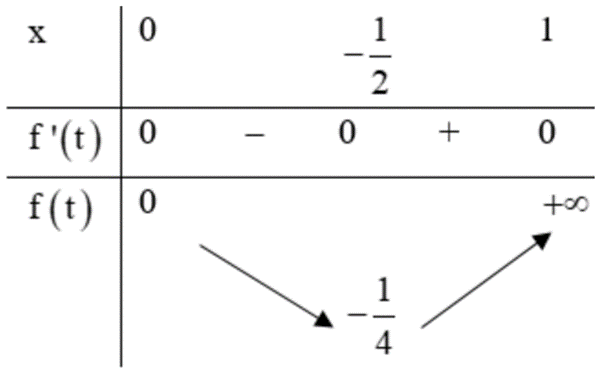
Ta có: f(0) = 0; \(f\left( { - \frac{1}{2}} \right) = - \frac{1}{4};\) \(\mathop {\lim }\limits_{t \to - \infty } f\left( t \right) = + \infty \).
Do đó để f(t) = -m có nghiệm thuộc khoảng (-∞; 0) ⇔ \( - m \ge - \frac{1}{4}\) ⇔ \(m \le \frac{1}{4}.\)

