Tìm tất cả các giá trị thực của tham số m để điểm M(2m3;m)

Câu hỏi:

Tìm tất cả các giá trị thực của tham số m để điểm $M (2 m^{3}; m)$ tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số $y = 2 x^{3} - 3 (2 m + 1) x^{2} + 6 m (m + 1) x + 1$ một tam giác có diện tích nhỏ nhất

A. m = 2

B. m = 0

C. m = 1

D. m = -1

Trả lời:

Chọn B

Ta có:

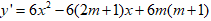
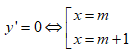
$\Rightarrow \forall m \in ℝ$ , hàm số luôn có CĐ, CT

Tọa độ các điểm CĐ, CT của đồ thị là

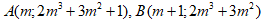
Suy ra $A B = \sqrt{2}$

và phương trình đường thẳng $x + y - 2 m^{3} - 3 m^{2} - m - 1 = 0$

Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.

Ta có:

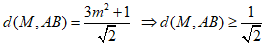
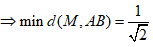
$\Rightarrow$ đạt được khi m = 0

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số $y = (m - 1) x^{4} - 3 m x^{2} + 5$ . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu

Xem lời giải »

Câu 2:

Cho hàm số $y = x^{4} - 2 (1 - m^{2}) x^{2} + m + 1$ . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất

Xem lời giải »

Câu 3:

Tìm các giá trị của tham số m để đồ thị hàm số $y = 2 x^{3} + 3 (m - 3) x^{2} + 11 - 3 m$ có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C(0;-1) thẳng hàng

Xem lời giải »

Câu 4:

Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: $y = x^{3} - 3 m x + 2$ cắt đường tròn tâm $I (1; 1)$ bán kính bằng 1 tại 2 điểm $A, B$ mà diện tích tam giác $I A B$ lớn nhất

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Tìm tất cả các giá trị thực của tham số m để điểm M(2m3;m)

Xem thêm bài tập Toán có lời giải hay khác: