Tìm tất cả các giá trị thực của tham số m để phương trình x^2 - 5x + 7 + 2m = 0
Câu hỏi:
Tìm tất cả các giá trị thực của tham số m để phương trình x2 – 5x + 7 + 2m = 0 có nghiệm thuộc đoạn [1; 5]
A. \(\frac{3}{4} \le m \le 7\)
B. \( - \frac{7}{2} \le m \le - \frac{3}{8}\)
C. \(3 \le m \le 7\)
D. \(\frac{3}{8} \le m \le \frac{7}{2}\).
Trả lời:
Đáp án đúng là: B
Ta có: x2 – 5x + 7 + 2m = 0
⇔ x2 – 5x + 7 = – 2m (*)
Phương trình (*) là phương trình hoành độ giao điểm của Parabol (P): x2 – 5x + 7 và đường thẳng y = – 2m (song song hoặc trùng với trục hoành)
Ta có bảng biến thiên của hàm số x2 – 5x + 7 trên đoạn [1; 5] như sau:
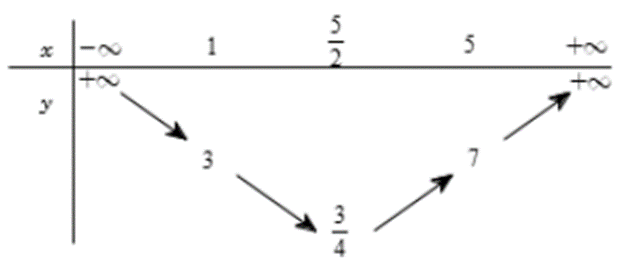
Dựa vào bảng biến thiên ta thấy x ∈ [1; 5] thì \(y \in \left[ {\frac{3}{4};7} \right]\)
Do đó để phương trình (*) có nghiệm x ∈ [1; 5]
\( \Leftrightarrow \frac{3}{4} \le - 2m \le 7 \Leftrightarrow \frac{{ - 3}}{8} \ge m \ge - \frac{7}{2}\)
Vậy ta chọn đáp án B.

