Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = mc^3/3 + 7mx^2
Câu hỏi:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = \frac{{m{x^3}}}{3} + 7m{x^2} + 14x - m + 2\) nghịch biến trên [1; +∞).
Trả lời:
Ta có: \(y = \frac{{m{x^3}}}{3} + 7m{x^2} + 14x - m + 2\)
Þ y¢ = mx2 + 14mx + 14
Hàm số đã cho nghịch biến trên [1; +∞) khi và chỉ khi
y¢ = mx2 + 14mx + 14 ≤ 0, "x Î [1; +∞)
Û m(x2 + 14x) ≤ −14, "x Î [1; +∞) (1)
\( \Leftrightarrow m \le - \frac{{14}}{{{x^2} + 14}},\;\forall x \in \left[ {1;\; + \infty } \right)\)
Đặt \(f\left( x \right) = - \frac{{14}}{{{x^2} + 14}},\;\forall x \in \left[ {1;\; + \infty } \right)\)
\( \Rightarrow f'\left( x \right) = \frac{{28x}}{{{{\left( {{x^2} + 14} \right)}^2}}} > 0,\;\forall x \in \left[ {1;\; + \infty } \right)\)
Suy ra hàm số đồng biến trên [1; +∞)
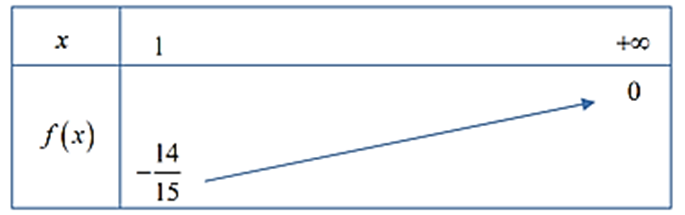
Nên \(\mathop {\min }\limits_{\left[ {1;\; + \infty } \right)} f\left( x \right) = f\left( 1 \right) = \frac{{ - 14}}{{15}}\).
Do đó để \(m \le - \frac{{14}}{{{x^2} + 14}},\;\forall x \in \left[ {1;\; + \infty } \right)\) thì \(m \le \mathop {\min }\limits_{\left[ {1;\; + \infty } \right)} f\left( x \right) \Rightarrow m \le \frac{{ - 14}}{{15}}\).
Vây với \(m \in \left( { - \infty ;\;\frac{{ - 14}}{{15}}} \right]\) thì hàm số nghịch biến trên nửa khoảng [1; +∞).

