Tìm x, y. z thuộc R thỏa mãn (x + 3y) / 19 = (3y + 9z) / 114 = (5z + 15x) / 115
Câu hỏi:
Tìm x, y. z ∈ ℝ thỏa mãn \(\frac{{x + 3y}}{{19}} = \frac{{3y + 9z}}{{114}} = \frac{{5z + 15x}}{{115}}\) và x + y + 2z = –31.
Trả lời:
Đặt \(\frac{{x + 3y}}{{19}} = \frac{{3y + 9z}}{{114}} = \frac{{5z + 15x}}{{115}} = t\)
⇒ x + 3y = 19t (1); 3y + 9z = 114t (2); 5z + 15x = 115t hay z + 3x = 23t (3)
Từ (1), (2), (3) ta có:
x = 4t, y = 5t, z = 11t
x + y + 2z = – 31
⇔ 4t + 5t + 11t = –31
⇔ 31t = – 31
⇔ t = –1
Suy ra: x = –4; y = –5; z = –11.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–1; 2); B(3; 2); C(1; 5). Tính tọa độ trọng tâm của tam giác ABC?
Xem lời giải »
Câu 2:
Trong mặt phẳng Oxy cho các điểm A(–1; 2); B(5; 8) điểm M thuộc Ox sao cho tam giác MAB vuông tại A. Tính diện tích tam giác MAB?
Xem lời giải »
Câu 3:
Cho các số x, y, z dương thoả mãn x2 + y2 + z2 = 1. Tìm giá trị nhỏ nhất của biểu thức M = \(\frac{1}{{16{x^2}}} + \frac{1}{{4{y^2}}} + \frac{1}{{{z^2}}}\).
Xem lời giải »
Câu 4:
Tìm số lớn nhất có 4 chữ số khác nhau, chữ số hàng trăm là chữ số 5. Số này phải chia hết cho 2 và chia hết cho 5.
Xem lời giải »
Câu 5:
Tìm góc tạo bởi đường thẳng y = 2x – 1 với trục Ox.
Xem lời giải »
Câu 7:
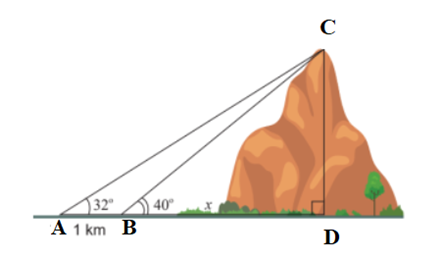
Tính chiều cao của một ngọn núi DC cho biết tại hai điểm A, B cách nhau 1km trên mặt đất ta nhìn thấy đỉnh núi với góc nâng lần lượt là 40° và 32° (làm tròn đến hai chữ số thập phân).
Xem lời giải »
Câu 8:
Tổng số học sinh của 1 trường THCS là 600 em học sinh. Tính số học sinh mỗi khối biết rằng số học sinh bốn khối 6, 7, 8, 9 cửa trường đó tỉ lệ nghịch với các số 9, 8, 7, 6.
Xem lời giải »