Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (–1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?
A. \[{\rm{d}} = - \frac{{\sqrt 3 }}{3}\]
B. \[{\rm{d}} = \sqrt 3 \]
C. \[{\rm{d}} = \frac{1}{3}\]
D. \[{\rm{d}} = \frac{1}{{\sqrt 3 }}\].
Trả lời:
Đáp án đúng là: D
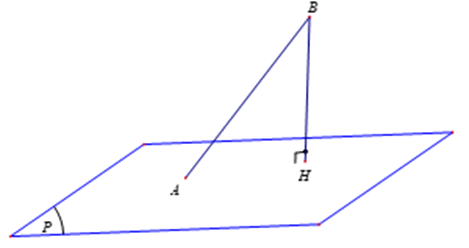
Ta có \(\overrightarrow {AB} = \left( {1; - 1;1} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = \sqrt 3 \)
Gọi H là hình chiếu của B trên mặt phẳng (P)
Khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P)
Ta luôn có BH ≤ AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A
Khi đó \(\overrightarrow {AB} = \left( {1; - 1;1} \right)\) là véc tơ pháp tuyến của mặt phẳng (P)
Suy ra phương trình mặt phẳng (P) đi qua A (–1; 2; 4) và có véc tơ pháp tuyến \(\overrightarrow {AB} = \left( {1; - 1;1} \right)\) là x – y + z – 1 = 0
Do đó khoảng cách từ điểm O đến mặt phẳng (P) là:
\(d\left( {O,\left( P \right)} \right) = \frac{{\left| { - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{1}{{\sqrt 3 }}\)
Vậy ta chọn đáp án D.

