Trong mặt phẳng Oxy, cho tam giác ABC biết A (-2; -3), B (1; 1), C (3: -3). Tìm điểm
Câu hỏi:
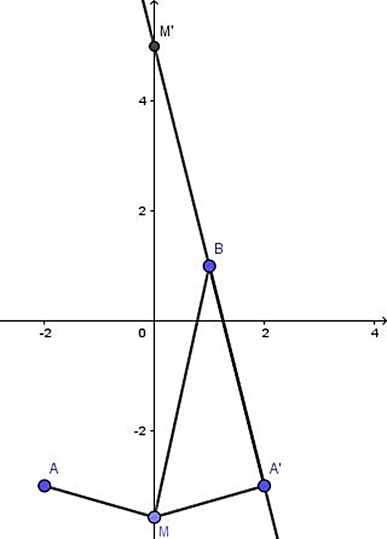
Trong mặt phẳng Oxy, cho tam giác ABC biết A (–2; –3), B (1; 1), C (3: –3). Tìm điểm M trên trục Oy sao cho \(\left| {MA - MB} \right|\) lớn nhất.
Trả lời:
Dễ thấy A và B nằm khác phía với trục Oy.
Gọi A’ là điểm đối xứng với A qua Oy. Khi đó A′(2;−3)
ở đó M′là giao điểm của A’B với Oy.
Gọi A’B: y = ax + b
A′(2;−3) ∈ A′B ⇔ −3 = 2a + b (1)
B(1;1) ∈ A′B ⇔ 1 = a + b (2)
Từ (1) và (2) suy ra: a = –4; b = 5 hay A′B: y = –4x + 5
Cho x = 0 thì y = 5
Suy ra M′ (0;5)
Vậy \(\left| {MA - MB} \right|\)max = A′B khi M trùng M′(0;5)