Biểu diễn các góc lượng giác trên đường tròn lượng giác: k pi/2 (k thuộc Z)
Câu hỏi:
Biểu diễn các góc lượng giác trên đường tròn lượng giác: \(k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
Trả lời:
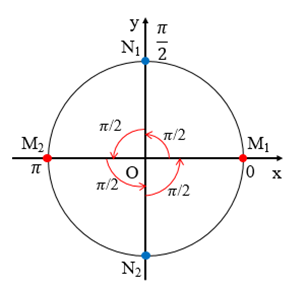
Câu hỏi:
Biểu diễn các góc lượng giác trên đường tròn lượng giác: \(k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
Trả lời:

Câu 1:
Tính tích phân\(\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\sqrt {1 + \sin x} dx} \).
Câu 3:
Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right|;\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right|\).
Câu 4:
Cho tam giác đều cạnh a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|;\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Câu 6:
Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm đi 84 m2.
Câu 7:
Cho ngũ giác đều ABCDE tâm O. Phép quay nào sau đây biến ngũ giác thành chính nó?
Câu 8:
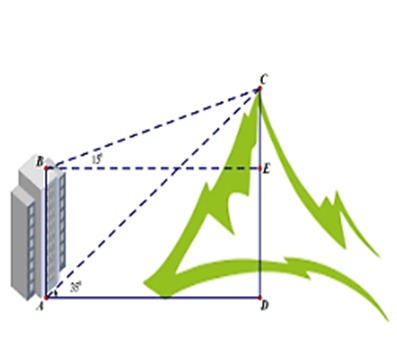
Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 60 m.