Cho điểm D nằm trong tam giác ABC sao cho góc DAB = góc DBC = góc DCA = phi. Chứng minh rằng: sin3φ = sin(A – φ). sin(B – φ). sin(C – φ).
Câu hỏi:
Cho điểm D nằm trong tam giác ABC sao cho \(\widehat {DAB} = \widehat {DBC} = \widehat {DCA} = \varphi \). Chứng minh rằng: sin3φ = sin(A – φ). sin(B – φ). sin(C – φ).
Trả lời:
Lời giải
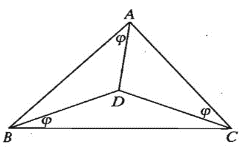
Theo định lý sin, trong tam giác ABD ta có:
\(\frac{{DB}}{{\sin \varphi }} = \frac{{AD}}{{\sin \left( {B - \varphi } \right)}}\)
Trong tam giác BCD có:
\(\frac{{CD}}{{\sin \varphi }} = \frac{{BD}}{{\sin \left( {C - \varphi } \right)}}\)
Trong tam giác ACD có:
\(\frac{{AD}}{{\sin \varphi }} = \frac{{CD}}{{\sin \left( {A - \varphi } \right)}}\)
Suy ra:
\(\frac{{B{\rm{D}}}}{{\sin \varphi }}.\frac{{C{\rm{D}}}}{{\sin \varphi }}.\frac{{A{\rm{D}}}}{{\sin \varphi }} = \frac{{AD}}{{\sin \left( {B - \varphi } \right)}}.\frac{{BD}}{{\sin \left( {C - \varphi } \right)}}.\frac{{CD}}{{\sin \left( {A - \varphi } \right)}}\)
Do đó: sin3φ = sin(A – φ). sin(B – φ). sin(C – φ)
Vậy sin3φ = sin(A – φ). sin(B – φ). sin(C – φ).
