Cho đường tròn (O; 25cm) và hai dây MN // PQ có độ dài theo thứ tự 40 cm và
Câu hỏi:
Cho đường tròn (O; 25cm) và hai dây MN // PQ có độ dài theo thứ tự 40 cm và 38 cm. Tính khoảng cách giữa dây MN và PQ?
Trả lời:
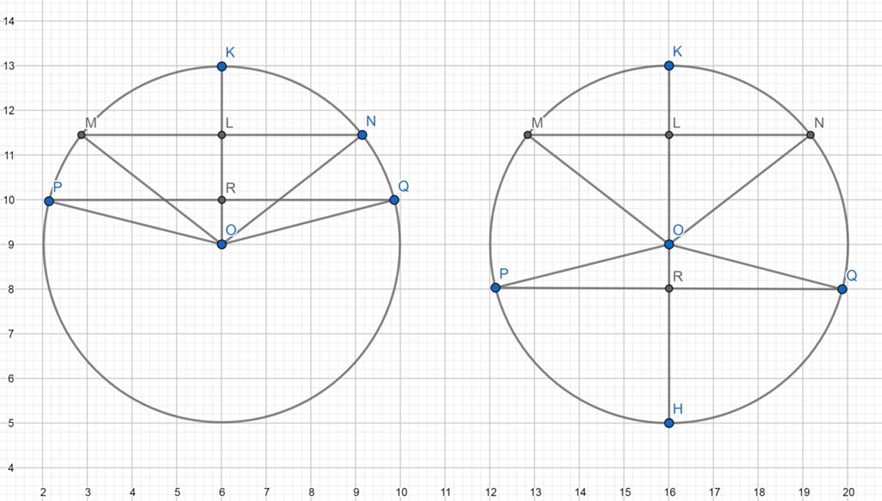
+) Trường hợp khi 2 dây cùng thuộc một mặt phẳng đường kính
Kẻ bán kính OK vuông góc 2 dây lần lượt tại R, L.
Suy ra: \(\left\{ \begin{array}{l}PR = RQ = \frac{1}{2}PQ = \frac{1}{2}.48 = 24\left( {cm} \right)\\LM = LN = \frac{1}{2}MN = \frac{1}{2}.40 = 20\left( {cm} \right)\end{array} \right.\)
Xét tam giác OPR vuông tại R có: RO2 + RP2 = OL2
⇒ RO = \(\sqrt {O{P^2} - R{P^2}} = \sqrt {{{25}^2} - {{24}^2}} = 7\left( {cm} \right)\)
Xét tam giác OLM vuông tại L có: LO2 + LM2 = OL2
⇒ LO = \(\sqrt {O{L^2} - L{M^2}} = \sqrt {{{25}^2} - {{20}^2}} = 15\left( {cm} \right)\)
Lại có: OR + RL = OL
⇒ RL = OL – OR = 15 – 7 = 8 (cm)
+) Trường hợp khi 2 dây không cùng thuộc một mặt phẳng đường kính
Kẻ bán kính OK, OH vuông góc 2 dây lần lượt tại R,L
Suy ra: \(\left\{ \begin{array}{l}PR = RQ = \frac{1}{2}PQ = \frac{1}{2}.48 = 24\left( {cm} \right)\\LM = LN = \frac{1}{2}MN = \frac{1}{2}.40 = 20\left( {cm} \right)\end{array} \right.\)
Xét tam giác OPR vuông tại R có: RO2 + RP2 = OL2
⇒ RO = \(\sqrt {O{P^2} - R{P^2}} = \sqrt {{{25}^2} - {{24}^2}} = 7\left( {cm} \right)\)
Xét tam giác OLM vuông tại L có: LO2 + LM2 = OL2
⇒ LO = \(\sqrt {O{L^2} - L{M^2}} = \sqrt {{{25}^2} - {{20}^2}} = 15\left( {cm} \right)\)
Lại có: OR + OL = RL
⇒ RL = OL + OR = 15 + 7 = 22 (cm).

