Cho đường tròn (O) đường kính AB, E thuộc đoạn AO (E khác A, O và AE
Câu hỏi:
Cho đường tròn (O) đường kính AB, E thuộc đoạn AO (E khác A, O và AE > EO). Gọi H là trung điểm của AE , kẻ dây CD vuông góc với AE tại H.
a) Tính góc ACB ?
b) Tứ giác ACED là hình gì ?
c) Gọi I là giao điểm của DE và BC . Chứng minh HI là tiếp tuyến của đường tròn đường kính EB ?
Trả lời:
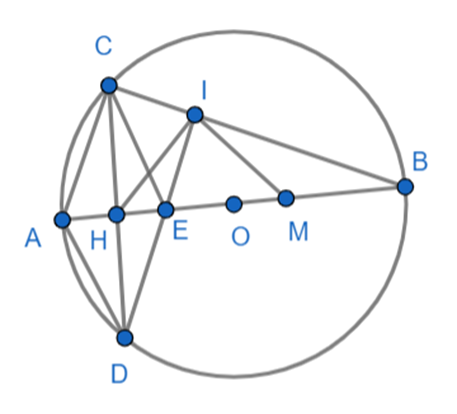
a) Vì \(\widehat {ACB}\)là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACB} = 90^\circ \)
b) Xét (O) có
OH là một phần đường kính
CD là dây
OH ⊥ CD tại H
Do đó: H là trung điểm của CD
Xét tứ giác ECAD có
H là trung điểm của đường chéo CD
H là trung điểm của đường chéo EA
Do đó: ECAD là hình bình hành
Mà EA ⊥ CD
Nên ECAD là hình thoi
c) ACED là hình thoi nên DE //AC
Mà AC ⊥ BC nên DE ⊥ BC
Suy ra: DI ⊥ BC
⇒ \(\widehat {EIB} = 90^\circ \)và \(\widehat {CID} = 90^\circ \)
Xét tam giác CID vuông tại I có IH là trung tuyến
⇒ IH = \(\frac{1}{2}CD = DH\)
⇒ ∆DHI cân tại H ⇒ \(\widehat {HID} = \widehat {EBI}\)
Gọi M là trung điểm BE
Suy ra: IM là trung tuyến của ∆IBE vuông tại I.
⇒ IM = \(\frac{1}{2}BE = BM\)
⇒ ∆MBI cân tại M
⇒ \(\widehat {MBI} = \widehat {MIB} = \widehat {EBI} = \widehat {HID}\)
Ta có: \(90^\circ = \widehat {EIB} = \widehat {BIM} + \widehat {EIM} = \widehat {HID} + \widehat {EIM} = \widehat {HIM}\)
Suy ra: HI ⊥ IM tại I
Vì IM = EM = BM = \(\frac{1}{2}BE\) và HI ⊥ IM nên HI là tiếp tuyến của \(\left( {M;\frac{{EB}}{2}} \right)\).

