Cho (O) đường kính AC . trên đoạn OC lấy điểm B và vẽ đường tròn tâm O'
Câu hỏi:
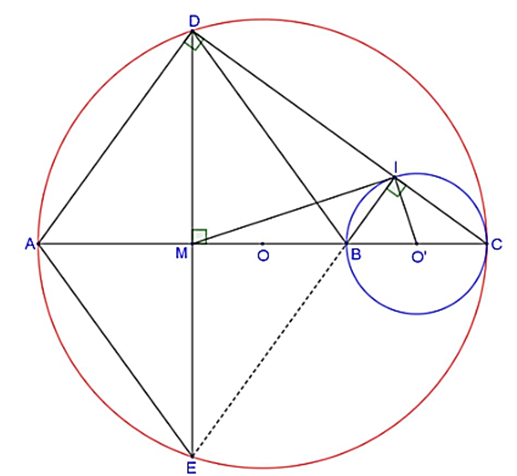
Cho (O) đường kính AC . trên đoạn OC lấy điểm B và vẽ đường tròn tâm O', đường kính BC. Gọi M là trung điểm của đoạn AB . Từ M vẽ dây cung DE vuông góc với AB, DC cắt đường tròn tâm O' tại I.
1. Tứ giác ADBE là hình gì?
2. Chứng minh DMBI nội tiếp.
3. Chứng minh B, I ,E Thẳng hàng và MI = MD.
4. Chứng minh MC.DB = MI.DC.
5. Chứng minh MI là tiếp tuyến của (O').
Trả lời:
1) Ta có OM ⊥ DE tại M
Nên M là trung điểm của DE(quan hệ đường kính – dây cung)
Xét tứ giác ADBE, ta có:
M là trung điểm của AB(gt)
M là trung điểm của DE(cmt)
AB ⊥ DE tại M (gt)
Nên tứ giác ADBE là hình thoi
2) Ta có: \(\widehat {BIC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Vậy tứ giác DMBI có \(\widehat {DMB} = \widehat {BIC} = 90^\circ \)
Nên DMBI nội tiếp (góc ngoài bằng góc đối trong)
3) Ta có \(\widehat {ADC} = \widehat {BIC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Nên AD ⊥ DC và BI ⊥ DC
⇒ AD // BI
Mà AD // BE (vì ADBE là hình thoi)
Do đó BI ≡ BE ⇒ B, I, E thẳng hàng
Vậy ΔDIEvuông tại I có IM là đường trung tuyến nên MI = MD
4) Vì DMBI nội tiếp nên \(\widehat {BMI} = \widehat {BDI}\)(cùng chắn cung BI)
Xét ΔMICΔ và ΔDBC, ta có:
\(\widehat {BMI} = \widehat {BDI}\)
\(\widehat {MCI}\)là góc chung
Nên ΔMIC ~ ΔDBC(g.g)
⇒ \(\frac{{MI}}{{DB}} = \frac{{MC}}{{DC}}\)
⇒ MC.DB = MI.DC
5) Ta có:
\[\widehat {MIB} = \widehat {MDB}\](vì DMBI nội tiếp)
\[\widehat {MDA} = \widehat {MDB}\](vì ADBE là hình thoi)
\[\widehat {MDA} = \widehat {BCI}\] (cùng phụ \(\widehat {DAM}\))
(trong (O′)
Nên (trong (O′)
Vậy MI là tiếp tuyến của (O′).

