Cho đường tròn (O; R), đường kính AB. Trên đường tròn (O) lấy điểm D sao cho
Câu hỏi:
Cho đường tròn (O; R), đường kính AB. Trên đường tròn (O) lấy điểm D sao cho AD > BD, D khác A và B. Kẻ OH vuông góc với AD tại H, tia OH cắt tiếp tuyến Ax của đường tròn (O) tại C.
a) Chứng minh H là trung điểm của AD và OH.OC = R².
b) Gọi E là giao điểm của BC và đưởng tròn (O). Chứng minh bốn điểm A, H, E, C cùng thuộc một đường tròn và CD là tiếp tuyến của đường tròn (O).Trả lời:
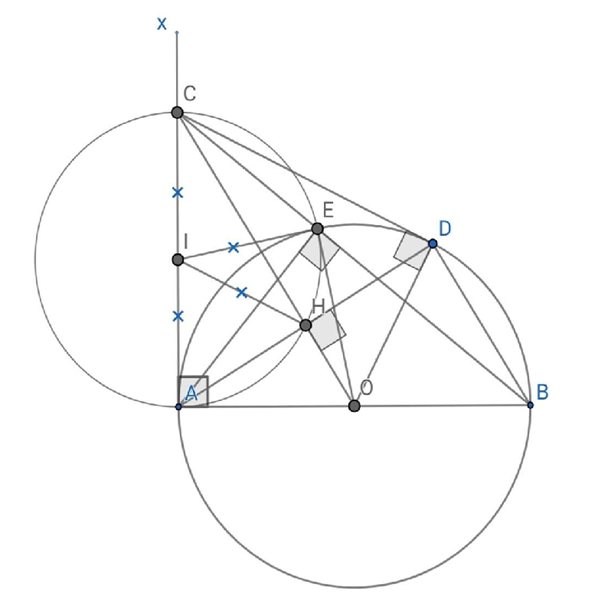
a) Ta có OA = OD = R
⇒ ΔAOD cân tại O
Vì OH ⊥ AD tại H (gt)
⇒ OH vừa là đường cao, trung tuyến và phân giác của ΔAOD
⇒ H là trung điểm AD
Áp dụng hệ thức lượng trong ΔACO vuông tại A có AH ⊥ OC
⇒ OH.OC = OA2 = R2
Vậy H là trung điểm AD và OH.OC = R2
b) ΔEAB nội tiếp (O;R) có AB là đường kính
⇒ ΔEAB vuông tại E
⇒ AE ⊥ BC tại E
⇒ ΔACE vuông tại E
Gọi I là trung điểm AC
⇒ EI là trung tuyến ΔACE
⇒ EI = AI = CI = \(\frac{1}{2}\)AC
HI là trung tuyến ΔACH vuông tại H
⇒ HI = \(\frac{1}{2}\)AC
⇒ AI = HI = EI = CI = \(\frac{1}{2}\)AC
⇒ A; H; E; C cùng thuộc đường tròn tâm I đường kính AC
Vì OH là phân giác của ΔAOD (câu a)
⇒ \(\widehat {DOC} = \widehat {AOC}\)
Xét ΔDOC và ΔAOC có:
OC là cạnh chung
\(\widehat {DOC} = \widehat {AOC}\)
OD = OA = R
⇒ ΔDOC = ΔAOC (c–g–c)
⇒ \(\widehat {CDO} = \widehat {CAO}\)= 90°
⇒ CD ⊥ OD
⇒ CD là tiếp tuyến tại D của (O).

