Cho đường tròn (O; R) và dây BC cố định (BC < 2R), BF là đường kính. A là
Câu hỏi:
Cho đường tròn (O; R) và dây BC cố định (BC < 2R), BF là đường kính. A là điểm di chuyển trên cung lớn BC (A khác B, C) sao cho tam giác ABC có ba góc nhọn, các đường cao AD và CE của tam giác ABC cắt nhau tại H.
a) Chứng minh AEDC nội tiếp.
b) Chứng minh HF đi qua trung điểm G của đoạn thẳng AC.
Trả lời:
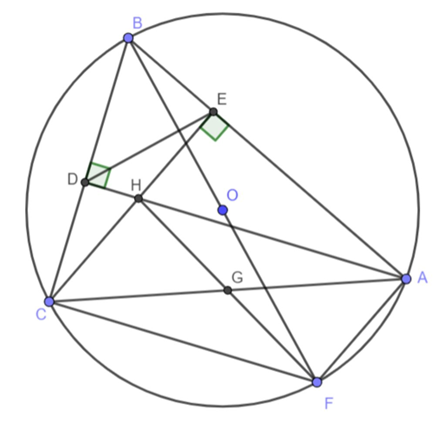
a) Ta có: \[\widehat {ADC} = \widehat {AEC} = 90^\circ \] (do AD, CE là đường cao của ΔABC)
⇒ D, E cùng nhìn cạnh AC dưới một góc là 90°
Nên AEDC nội tiếp đường tròn đường kính (AC).
b) Ta có BF ta đường kính (O)
nên \(\widehat {BAF}\) = 90° (góc nội tiếp chắn nửa đường tròn (O))
⇒ FA ⊥ AB
⇒ CH // FA (do cùng vuông góc với AB)
Tương tự \(\widehat {BCF}\) = 90°
⇒ AH // CF do cùng ⊥ BC
⇒ AHCF là hình bình hành hai đường chéo AC, HF cắt nhau tại trung điểm mỗi đường mà G là trung điểm của AC nên G là trung điểm của HF.

