Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm. a) Tính khoảng cách
Câu hỏi:
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.
Trả lời:
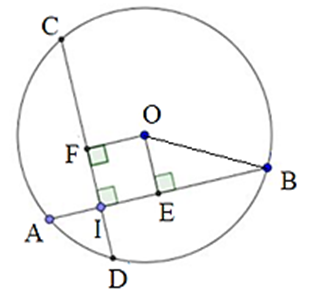
Kẻ OE ⊥ AB tại E
OE là một phần của đường kính
Do đó, E là trung điểm của đoạn thẳng AB
⇒ EA = EB = \(\frac{1}{2}AB = \frac{1}{2}.8\)= 4 (cm)
Xét tam giác OEB vuông tại E (do OE ⊥ AB)
Áp dụng định lí Py–ta–go ta có:
OB2 = OE2 + EB2
OE2 = 52 – 42 = 9
OE = 3(cm)
Vậy khoảng cách từ tâm O đến dây AB là 3cm.
b) Kẻ OF ⊥ CD tại F
Xét tứ giác FOEI
\(\widehat {FIE}\)= 90° (do AB⊥CD tại I)
\(\widehat {IFO}\) = 90° (do OF⊥CD tại F)
\(\widehat {IEO}\) = 90° (do OE⊥AB tại E)
Do đó, tứ giác FOEI là hình chữ nhật
⇒ OF = EI
Ta có:
EA = 4cm
AI = 1cm
⇒ EI = EA – AI = 4 – 1 = 3 (cm)
⇒ OF = EI = 3cm
⇒ OF = OE = 3cm
Vậy hai dây AB và CD cách đều tâm, do đó chúng bằng nhau, tức là AB = CD.

