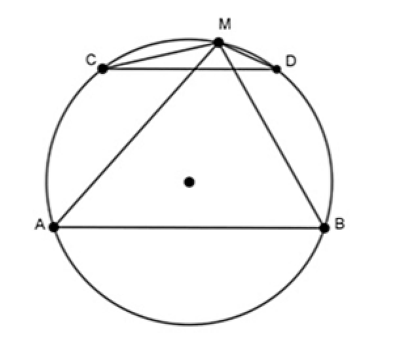
Cho đường tròn tâm O và hai dây cung song song AB, CD. Trên cung AB lấy điểm M. Chứng minh rằng .

Tìm x, y > 0 biết x – y = 7 và xy = 60.

Tìm số tự nhiên n biết 3ⁿ + 4ⁿ = 5ⁿ.

Tìm x sao cho x⁴ + 2x³ + 2x² + x + 3 là số chính phương.

Bốn bạn cùng chạy trên một quãng đường và cùng xuất phát một lúc. Khi đến đích tính ra bạn Sơn chạy hết 81 giây; bạn Tùng chạy hết 1,4 phút, bạn Thông chạy hết $1\frac{4}{9}$  phút, bạn Bách chạy hết 1 phút 20 giây. Bạn chạy với vận tốc bé nhất (hay bạn chạy chậm nhất) là bạn nào?

Cho a, b, c ≥ 0 và thỏa mãn a² + b² + c² + abc = 4. Chứng minh abc + 2 ≥ ab + bc + ca ≥ abc.

Cho tam giác ABC vuông tại A, nội tiếp đường tròn tâm O, bán kính R = 3cm, biết sin  B= $\frac{2}{3}$  .

a) Hai dây AB và AC, dây nào gần tâm O hơn?

b) Một đường thẳng qua O, song song với AC cắt AB tại I, tính IB và IO.