Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD. a) Chứng minh AD = BC. b) Gọi E là giao điể
Câu hỏi:
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD.
a) Chứng minh AD = BC.
b) Gọi E là giao điểm của AD và BC. Chứng minh ∆EAC = ∆EBD.
c) Chứng minh OE là phân giác của \(\widehat {xOy}\).
Trả lời:
Lời giải
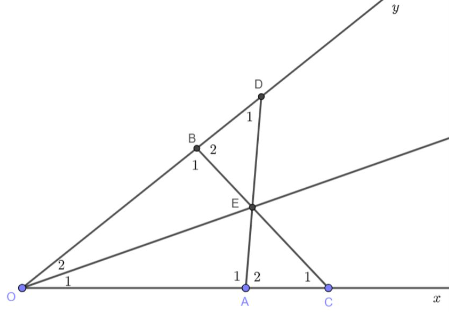
a) Ta có OA = OB và AC = BD.
Suy ra OA + AC = OB + BD.
Do đó OC = OD.
Xét ∆OAD và ∆OBC, có:
\(\widehat {AOD}\) là góc chung;
OA = OB (giả thiết);
OD = OC (chứng minh trên).
Do đó ∆OAD = ∆OBC (c.g.c).
Vậy AD = BC (cặp cạnh tương ứng).
b) Ta có \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) và \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (các cặp góc kề bù).
Mà \(\widehat {{A_1}} = \widehat {{B_1}}\) (do ∆OAD = ∆OBC).
Suy ra \(\widehat {{A_2}} = \widehat {{B_2}}\).
Xét ∆EAC và ∆EBD, có:
AC = BD (giả thiết);
\(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh trên);
\(\widehat {{C_1}} = \widehat {{D_1}}\) (do ∆OAD = ∆OBC).
Vậy ∆EAC = ∆EBD (g.c.g).
c) Xét ∆OED và ∆OEC, có:
OE là cạnh chung;
OD = OC (chứng minh trên);
ED = EC (do ∆EAC = ∆EBD).
Do đó ∆OED = ∆OEC (c.c.c).
Suy ra \(\widehat {{O_1}} = \widehat {{O_2}}\) (cặp góc tương ứng).
Vậy OE là phân giác của \(\widehat {xOy}\).

