Tính diện tích hình thang ABCD, biết AB // CD, góc D = 90^0, góc C = 38^0, AB = 3,5 cm, AD = 3,1 cm.
Câu hỏi:
Tính diện tích hình thang ABCD, biết AB // CD, \(\widehat D = 90^\circ \), \(\widehat C = 38^\circ \), AB = 3,5 cm, AD = 3,1 cm.
Trả lời:
Lời giải
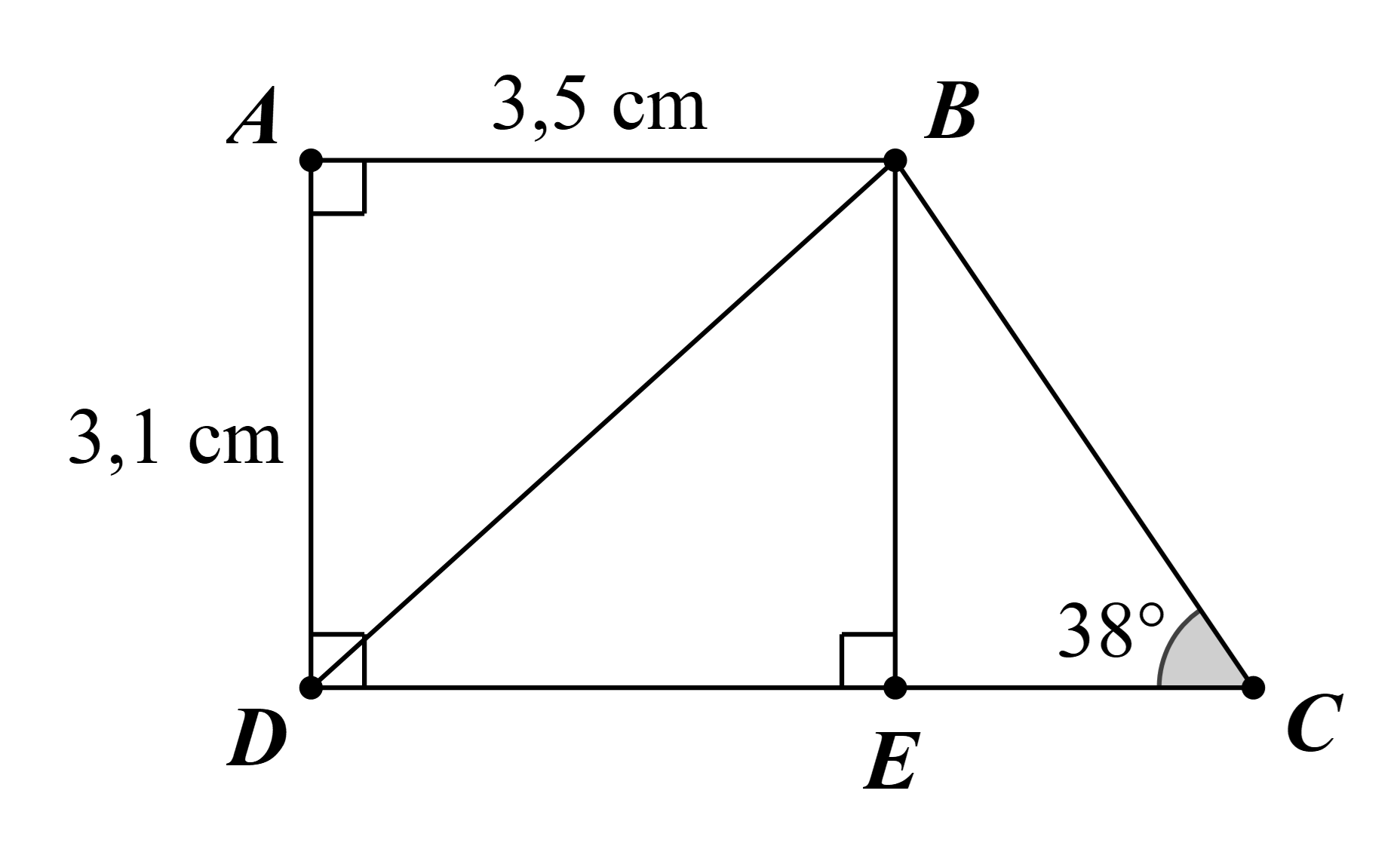
Kẻ BE ⊥ CD tại E.
Ta có AB // CD và AD ⊥ DC.
Suy ra AB ⊥ AD.
Khi đó tứ giác ABED là hình chữ nhật.
Vì vậy DE = AB = 3,5 cm và BE = AD = 3,1 cm.
Tam giác BEC vuông tại E: \(EC = \frac{{BE}}{{\tan \widehat {BCE}}} = \frac{{3,1}}{{\tan 38^\circ }} \approx 3,97\) (cm).
Khi đó DC = DE + EC ≈ 3,5 + 3,97 ≈ 7,47 (cm).
Diện tích hình thang ABCD là:
\(S = \frac{{AD.\left( {AB + DC} \right)}}{2} \approx \frac{{3,1.\left( {3,5 + 7,47} \right)}}{2} \approx 17,0035\) (cm2).
Vậy diện tích hình thang ABCD bằng 17,0035 cm2.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số f(x) = mx + m – 1. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = 0 có nghiệm thuộc (3; 4).
Xem lời giải »
Câu 2:
Cho hình bình hành ABCD có AC vuông góc AD, AD = 3,5 cm, \(\widehat D = 60^\circ \). Tính diện tích hình bình hành ABCD.
Xem lời giải »
Câu 3:
Một cửa hàng giảm giá 10% so với giá bán bình thường nhưng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì lãi bao nhiêu phần trăm so với giá vốn?
Xem lời giải »
Câu 4:
Cho a, b > 0 và a + b = 1. Chứng minh rằng \(\frac{1}{{{a^2} + {b^2}}} \ge 2\).
Xem lời giải »
Câu 5:
Cho lăng trụ ABC.A’B’C’ có cạnh bên bằng 2a, đáy ABC là tam giác vuông tại A, AB = a, \(AC = a\sqrt 3 \). Hình chiếu vuông góc của A’ lên (ABC) trùng với trung điểm I của BC. Tính khoảng cách giữa BB’ và AC’.
Xem lời giải »


