Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là AB. Lấy M, N lần lượt thuộc các cạnh SC, SD. Tìm thiết diện của hình chóp với các mặt phẳng (ABM) và (AMN).
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là AB. Lấy M, N lần lượt thuộc các cạnh SC, SD. Tìm thiết diện của hình chóp với các mặt phẳng (ABM) và (AMN).
Trả lời:
Lời giải
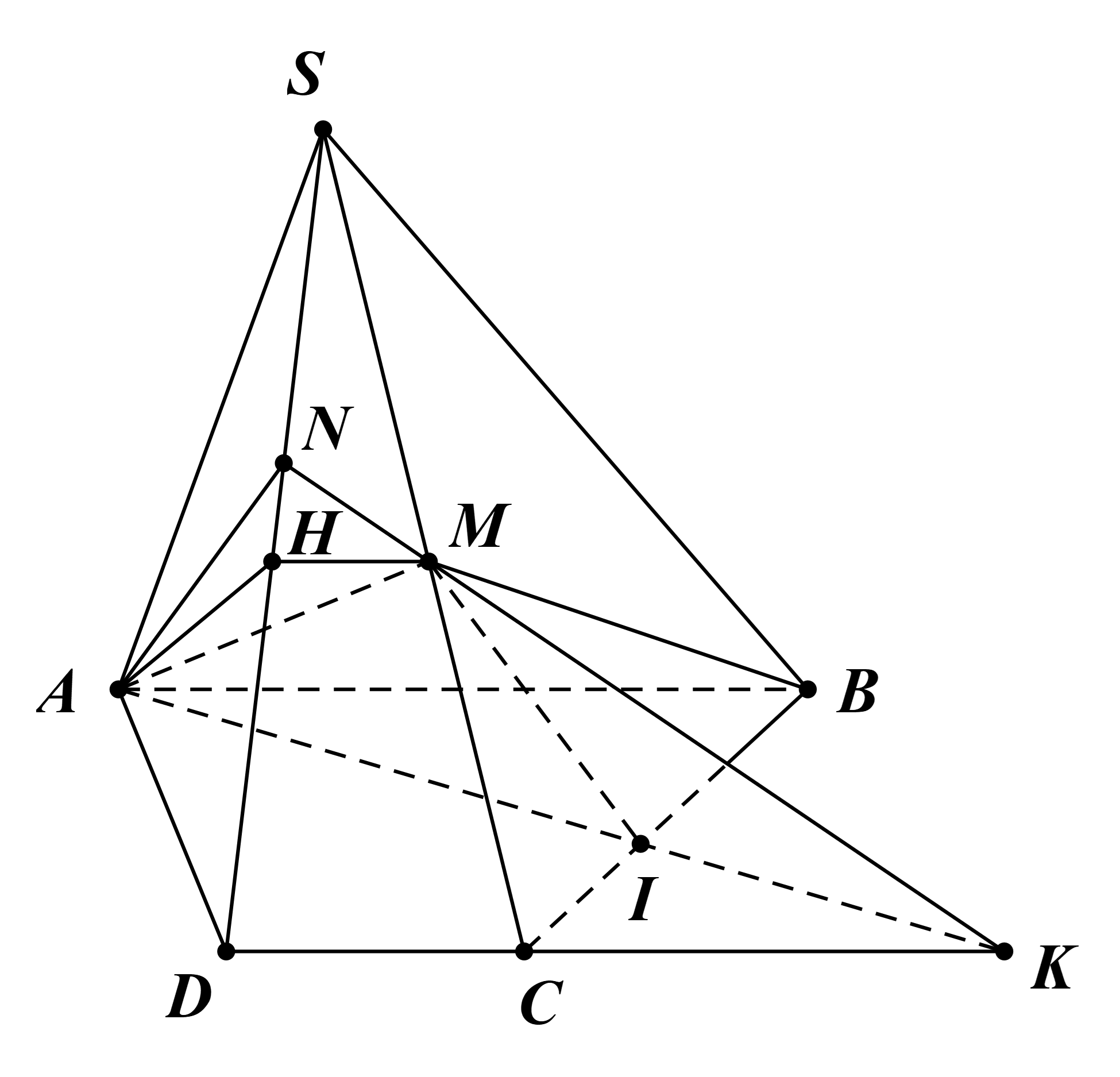
⦁ Thiết diện của hình chóp với (ABM):
Ta có M ∈ (ABM) ∩ (SCD).
Mà AB // CD.
Suy ra giao tuyến của hai mặt phẳng (ABM) và (SCD) là đường thẳng d đi qua M và d // AB // CD.
Trong (SCD): gọi H = d ∩ SD.
Suy ra MH = (ABM) ∩ (SCD).
Ta có:
+ (ABM) ∩ (ABCD) = AB.
+ (ABM) ∩ (SBC) = BM.
+ (ABM) ∩ (SCD) = MH.
+ (ABM) ∩ (SAD) = HA.
Vậy thiết diện của hình chóp với (ABM) là tứ giác ABMH.
⦁ Thiết diện của hình chóp với (AMN):
Trong (SCD): gọi K = MN ∩ CD.
Trong (ABCD): gọi I = AK ∩ BC.
Ta có:
+ (AMN) ∩ (SAD) = AN.
+ (AMN) ∩ (SCD) = MN.
+ (AMN) ∩ (SBC) = MI.
+ (AMN) ∩ (ABCD) = IA.
Vậy thiết diện của hình chóp với (AMN) là tứ giác ANMI.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số f(x) = mx + m – 1. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = 0 có nghiệm thuộc (3; 4).
Xem lời giải »
Câu 2:
Tính diện tích hình thang ABCD, biết AB // CD, \(\widehat D = 90^\circ \), \(\widehat C = 38^\circ \), AB = 3,5 cm, AD = 3,1 cm.
Xem lời giải »
Câu 3:
Cho hình bình hành ABCD có AC vuông góc AD, AD = 3,5 cm, \(\widehat D = 60^\circ \). Tính diện tích hình bình hành ABCD.
Xem lời giải »
Câu 4:
Một cửa hàng giảm giá 10% so với giá bán bình thường nhưng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì lãi bao nhiêu phần trăm so với giá vốn?
Xem lời giải »
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–2; 3), C(3; 1). Tìm tọa độ điểm A sao cho tam giác ABC vuông cân tại A.
Xem lời giải »
Câu 6:
Cho tam giác ABC có \(\widehat A = 60^\circ \), phân giác AD. Chứng minh rằng \(AD = \frac{{\sqrt 3 AB.AC}}{{AB + AC}}\).
Xem lời giải »
Câu 7:
Cho tam giác ABC có AB = AC. Trên hai cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = AN. Gọi E và D lần lượt là trung điểm của MN và BC. Chứng minh ba điểm A, E, D thẳng hàng.
Xem lời giải »
Câu 8:
Cho tứ diện OABC có OA vuông góc với (OBC) và OA = OB = 2OC, \(\widehat {BOC} = 60^\circ \). Gọi M là trung điểm của BC. Tính côsin giữa hai đường thẳng OM và AB.
Xem lời giải »


