Cho hàm số đồng biến trên và xác định tại hai điểm . Chọn kết luận đúng

Câu 1:

Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:

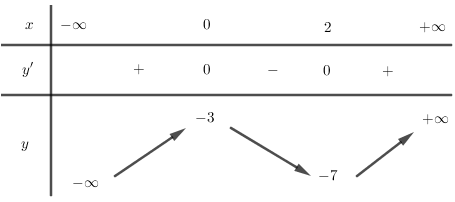
Xem lời giải »

Câu 2:

Cho hàm số $y=f\left(x\right)$ xác định, liên tục trên R và có bảng biến thiên sau:

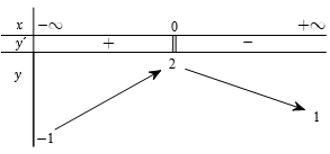
Khẳng định nào sau đây là đúng?

Xem lời giải »

Câu 3:

Cho hàm số $y=f\left(x\right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?

Xem lời giải »

Câu 4:

Cho hàm số $y=f\left(x\right)$ liên tục trên $\left[-1;3\right]$ và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=f\left(x\right)$ trên đoạn $\left[-1;3\right]$. Tính M – m.

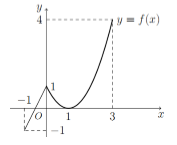
Xem lời giải »

Câu 5:

Cho hàm số f (x) xác định và liên tục trên R, có $\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty ;\underset{x\to -\infty }{\lim }f\left(x\right)=-\infty$, khi đó:

Xem lời giải »

Câu 6:

Cho hàm số $y=f\left(x\right)$ xác định và liên tục trên R, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số $y=f\left(x\right)$ trên đoạn $\left[-2;2\right]$

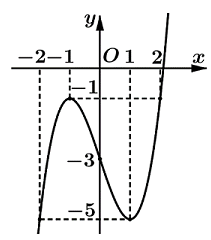
Xem lời giải »

Câu 7:

Giá trị lớn nhất của hàm số $f\left(x\right)=\frac{6-8x}{x^2+1}$ trên tập xác định của nó là:

Xem lời giải »

Câu 8:

Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y=x^4+2x^2-1$ trên đoạn $\left[-1;2\right]$ lần lượt là M và m. Khi đó giá trị của M.m là:

Xem lời giải »