Cho hàm số f(x) = (ax + 1) / (bx + c) (a, b, c thuộc R) có bẳng biến thiên như sau
Câu hỏi:
Cho hàm số \(f\left( x \right) = \frac{{ax + 1}}{{bx + c}}\;\left( {a,\;b,\;c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
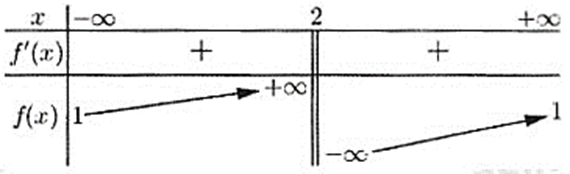
Trong các số a, b và c có bao nhiêu số dương?
Trả lời:
Dựa vào BBT ta thấy đồ thị hàm số có TCĐ: \(x = 2 \Rightarrow - \frac{c}{b} = 2 \Leftrightarrow c = - 2b\)
TCN: \(y = 1 \Rightarrow \frac{a}{b} = 1 \Leftrightarrow a = b\)
Ta có: \(f\left( x \right) = \frac{{ax + 1}}{{bx + c}} \Rightarrow f'\left( x \right) = \frac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}}\)
Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞)
Û y′ > 0, "x ¹ 2
\( \Leftrightarrow \frac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}} > 0,\;\forall x \ne 2\)
Û ac − b > 0
Û b.( −2b) − b > 0
Û −2b2 − b > 0
Û 2b2 + b < 0
\( \Leftrightarrow - \frac{1}{2} < b < 0\)
Þ b < 0 Þ a < 0, c > 0
Vậy trong ba số a, b, c có 1 số dương.

