Cho hàm số y = ax^3 + bx^2 +cx + d với a, b, c, d là các số thực và a khác 0

Câu hỏi:

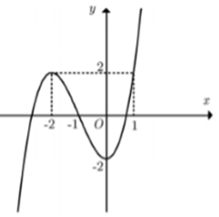
Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ với a, b, c, d là các số thực và a khác 0 (có đồ thị như hình vẽ). Khẳng định nào sau đây sai?

A. $y' < 0, \forall x \in (- 2; 0)$

B. Hàm số đạt GTNN tại điểm x = - 2

C. Đồ thị hàm số có đúng 2 điểm cực trị

D. $y' (x) = 0 \Leftrightarrow [\begin{matrix} x = - 2 \\ x = 0 \end{matrix}$

Trả lời:

Đáp án B

Đáp án A đúng. Ta thấy hàm số nghịch biến trên $(0; 2) \Rightarrow y' < 0, \forall x \in (0; 2)$

Đáp án B sai. Hàm số không có GTLN.

Đáp án C đúng. Hàm số có hai điểm cực trị x = - 2 và x = 0.

Đáp án D đúng.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Hình dưới đây là đồ thị của hàm số nào?

Xem lời giải »

Câu 2:

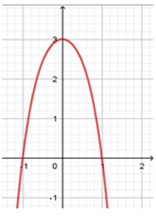
Đồ thị bên là đồ thị của hàm số nào trong các hàm số sau:

Xem lời giải »

Câu 3:

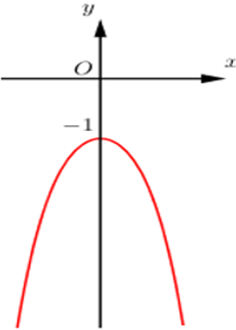
Đường cong hình bên là đồ thị hàm số nào dưới đây:

Xem lời giải »

Câu 4:

Đồ thị sau đây là của hàm số nào?

Xem lời giải »

Câu 5:

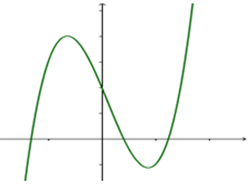
Cho hàm số $y = a x^{3} + b x^{2} + c x + d (a \neq 0)$ có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây về dấu của a, b, c, d là đúng nhất?

Xem lời giải »

Câu 6:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây là đúng?

Xem lời giải »

Câu 7:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây là đúng ?

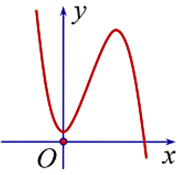
Xem lời giải »

Câu 8:

Hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?

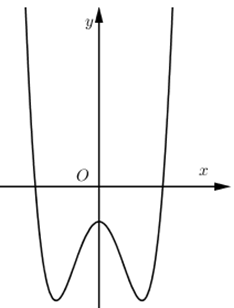
Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số y = ax^3 + bx^2 +cx + d với a, b, c, d là các số thực và a khác 0

Xem thêm bài tập Toán có lời giải hay khác: