Cho hàm số y = ax^4 + bx^2 + c (a = 1) có đồ thị (C), biết rằng (C) đi qua A(-1; 0)
Câu hỏi:
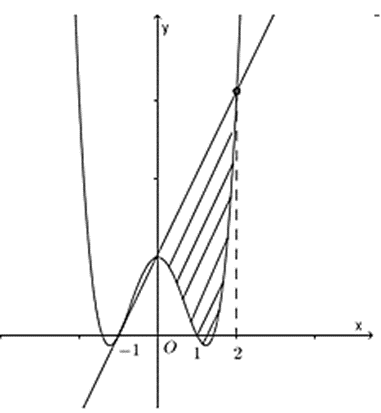
Cho hàm số y = ax4 + bx2 + c (a = 1) có đồ thị (C), biết rằng (C) đi qua A(−1; 0), tiếp tuyến d tại A của (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng \(\frac{{28}}{5}\) (phần gạch chéo trong hình vẽ). Tính diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = −1; x = 0.
Trả lời:
Đồ thị hàm số đi qua điểm (−1; 0); (1; 0) nên ta có:
y = (x2 − 1)(x2 − m) = x4 − (1 + m)x2 + m (m > 1)
y¢ = 4x3 − 2(1 + m)x = 2x(2x2 − 1 − m)
y¢(−1) = −2(1 − m) = 2m − 2
Phương trình tiếp tuyến tại A(−1; 0) có phương trình y = (2m − 2)(x + 1)
\(\int\limits_0^2 {\left[ {\left( {2m - 2} \right)\left( {x + 1} \right) - \left( {{x^4} - \left( {1 + m} \right){x^2} + m} \right)} \right]dx} = \frac{{28}}{5}\)
\[ \Leftrightarrow \left. {\left( {2m - 2} \right)\left( {\frac{{{x^2}}}{2} + x} \right)\;} \right|_0^2 - \;\left. {\left( {\frac{{{x^5}}}{5} - \left( {1 + m} \right)\frac{{{x^3}}}{3} + mx} \right)\;} \right|_0^2 = \frac{{28}}{5}\]
\[ \Leftrightarrow 4\left( {2m - 2} \right) + \frac{8}{5} - 2m = \frac{{28}}{5}\]
Û 6m = 12 Û m = 2
Khi đó hàm số (C) có dạng: y = (x2 − 2)(x2 − 1) = x4 − 3x2 + 2
Phương trình tiếp tuyến tại A có dạng: y = 2x + 2
\(S = \int\limits_{ - 1}^0 {\left( {{x^4} - 3{x^2} + 2 - 2x - 2} \right)dx} = \int\limits_{ - 1}^0 {\left( {{x^4} - 3{x^2} - 2x} \right)dx} \)
\( = \left. {\left( {\frac{{{x^5}}}{5} - {x^3} - {x^2}} \right)\;} \right|_{ - 1}^0 = \frac{1}{5} - 1 + 1 = \frac{1}{5}\).