Cho hàm số y = f (x) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình f (x + 2019)
Câu hỏi:
Cho hàm số y = f (x) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình f (x + 2019) = 1 là:
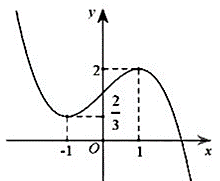
Trả lời:
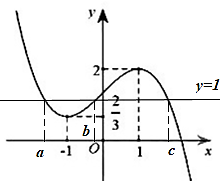
Dựa vào đồ thị hàm số ta thấy: Đường thẳng y = 1 cắt đồ thị hàm số y = f (x) tại 3 điểm phân biệt nên phương trình f (x + 2019) = 1 có 3 nghiệm phân biệt.
Vậy số nghiệm thực của phương trình f (x + 2019) = 1 là: 3 nghiệm.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Đa thức P (x) = 32x5 − 80x4 + 80x3 − 40x2 + 10x − 1 là khai triển của nhị thức nào dưới đây?
Xem lời giải »
Câu 2:
Cho đoạn thẳng AB. Vị trí của điểm M thỏa mãn: được xác định bởi:
Xem lời giải »
Câu 3:
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Xem lời giải »
Câu 4:
Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng: .
Xem lời giải »
Câu 5:
Cho hàm số f (x) liên tục trên ℝ và thoả mãn f (x) + f (−x) = 3 − 2cos x, với mọi x Î ℝ. Tính tích phân ?
Xem lời giải »
Câu 6:
Cho hàm số f (x) liên tục trên ℝ và thoả mãn
. Tính .
Xem lời giải »
Câu 7:
Cho hàm số f (x) liên tục trên ℝ và . Tính .
Xem lời giải »
Câu 8:
Cho f (x) liên tục trên ℝ và f (2) = 16, . Tích phân bằng:
Xem lời giải »



