Cho hàm số y = f(x) = x3 – 3x2 + m,∀m ∈ R

Câu hỏi:

Cho hàm số y = f(x) = x³ – 3x² + m,∀m ∈ R. Tìm tham số m để hàm số có giá trị cực đại bằng 2

A. m = 2

B. m = -2

C. m = -4

D. m = 0

Trả lời:

Đáp án A

Xét hàm số y = f(x) = x³ – 3x² + m, D = R.

f’(x) = 3x² – 6x

Cho f’(x) = 0 <=> 3x² – 6x = 0 <=>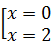

BBT

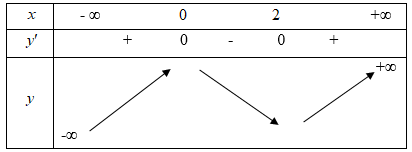
Suy ra hàm số đạt cực đại tại x = 0

Theo YCBT ta có f(0) = 2 $\Leftrightarrow$ m = 2

Câu 1:

Biết rằng đồ thị hàm số $y = \frac{x + 3}{x - 1}$ và đường thẳng y = x – 2 cắt nhau tại hai điểm phân biệt A(x_A;y_A) và B(x_B;y_B). Tính y_A + y_B.

Câu 2:

Tung độ giao điểm của đồ thị các hàm số y = x³ – 3x² + 2, y = -2x + 8 là:

Câu 3:

Có bao nhiêu điểm M thuộc đồ thị hàm số $y = \frac{x + 2}{x - 1}$ sao cho khoảng cách từ M đến trục tung bằng hai lần khoảng cách từ M đến trục hoành

Câu 4:

Cho hàm số $y = \frac{2 x + 1}{x - 1}$ Khẳng định nào sau đây là khẳng định sai?

Câu 5:

Tìm tất cả các giá trị của tham số m để hàm số y = -x³ + 2x² + mx đạt cực đại tại x = 1

Câu 6:

x = 2 không phải là điểm cực đại của hàm số nào sau đây?

Câu 7:

Hàm số y = x³/3 – (m + 1)x² + (2m² + 1)x + m đạt cực tiểu tại x = 1 khi

Câu 8:

Tập hợp tất cả các giá trị của tham số thực m sao cho hàm số $y = \frac{x^{2} + x + m^{2}}{x + 1}$ đạt cực đại tại x = 1 là

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án