Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f'(x) như

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho hàm số y = f(x) có đạo hàm liên tục trên $ℝ$ . Đồ thị hàm số y = f'(x) như hình vẽ sau:

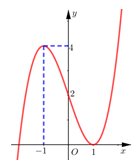
Số điểm cực trị của hàm số $y = f (x) - 4 x$ là

A. 2

B. 3

C. 4

D. 1

Trả lời:

Đáp án D

Đặt: $g (x) = f (x) - 4 x$

Ta có: $g^{'} (x) = f^{'} (x) - 4, g^{'} (x) = 0 \Leftrightarrow f^{'} (x) = 4$

Dựa vào đồ thị, suy ra phương trình $f^{'} (x) = 4$ có 2 nghiệm $x_{1}; x_{2}$ trong đó $x_{1} = - 1$ là nghiệm kép và $x_{2} > 1$ là nghiệm đơn.

$\Rightarrow$ Phương trình $g^{'} (x) = 0$ có 2 nghiệm $x_{1}; x_{2}$ nhưng $g^{'} (x)$ đổi dấu duy nhất 1 lần khi qua nghiệm $x_{2}$ này. Vậy hàm số $y = f (x) - 4 x$ có một điểm cực trị.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tìm m đề đồ thị hàm số $y = x^{4} - 2 m x^{2} + 1$ có ba điểm cực trị $A (0; 1), B, C$ thỏa mãn BC = 4

Xem lời giải »

Câu 2:

Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y = x^{4} - 2 (m + 1) x^{2} + m^{2}$ có ba điểm cực trị tạo thành một tam giác vuông cân

Xem lời giải »

Câu 3:

Cho hàm số y = f(x) có đúng ba điểm cực trị là $x = - 2, x = - 1, x = 2$ và có đạo hàm liên tục trên $ℝ$ .Khi đó hàm số $y = f (x^{2} - 2)$ có bao nhiêu điểm cực trị?

Xem lời giải »

Câu 4:

Gọi S là tập chứa tất cả các giá trị nguyên của m sao cho hàm số $y = x^{4} - 2 (m - 1) x^{2} + m^{2} - m$ có ba điểm cực trị lập thành một tam giác vuông. Tổng tất cả các phần tử của tập S bằng

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f'(x) như

Xem thêm bài tập Toán có lời giải hay khác: