Cho hàm số y = f(x) có đúng ba điểm cực trị là x = -2, x = -1, x = 2 và có

Câu hỏi:

Cho hàm số y = f(x) có đúng ba điểm cực trị là $x = - 2, x = - 1, x = 2$ và có đạo hàm liên tục trên $ℝ$ .Khi đó hàm số $y = f (x^{2} - 2)$ có bao nhiêu điểm cực trị?

A. 5

B. 8

C. 6

D. 4

Trả lời:

Đáp án A

Vì hàm số y = f(x) có đúng ba điểm cực trị là x = -2, x = -1, x = 2 và có đạo hàm liên tục trên $ℝ$ nên f'(x) = 0 có ba nghiệm là x = -2, x = -1, x = 2 (ba nghiệm bội lẻ).

Xét hàm số $g (x) = f (x^{2} - 2)$ có $g^{'} (x) = 2 x . f^{'} (x^{2} - 2)$

$g^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ f^{'} (x^{2} - 2) = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} - 2 = - 2 \\ x^{2} - 2 = - 1 \\ x^{2} - 2 = 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm 1 \\ x = \pm 2 \end{array}$

Do $g^{'} (x) = 0$ có các nghiệm bội lẻ $x = \pm 1; x = \pm 2; x = 0$ suy ra $g^{'} (x)$ đổi dấu năm lần nên hàm số $y = f (x^{2} - 2)$ có năm điểm cực trị.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số y = f(x) có đạo hàm liên tục trên $ℝ$ . Đồ thị hàm số y = f'(x) như hình vẽ sau:

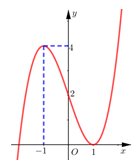
Số điểm cực trị của hàm số $y = f (x) - 4 x$ là

Xem lời giải »

Câu 2:

Tìm m đề đồ thị hàm số $y = x^{4} - 2 m x^{2} + 1$ có ba điểm cực trị $A (0; 1), B, C$ thỏa mãn BC = 4

Xem lời giải »

Câu 3:

Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y = x^{4} - 2 (m + 1) x^{2} + m^{2}$ có ba điểm cực trị tạo thành một tam giác vuông cân

Xem lời giải »

Câu 4:

Gọi S là tập chứa tất cả các giá trị nguyên của m sao cho hàm số $y = x^{4} - 2 (m - 1) x^{2} + m^{2} - m$ có ba điểm cực trị lập thành một tam giác vuông. Tổng tất cả các phần tử của tập S bằng

Xem lời giải »

Câu 5:

Cho hàm số y = f(x) có đạo hàm trên $ℝ$ và có bảng xét dấu f'(x) như sau

Hỏi hàm số $y = f (x^{2} - 2 x)$ có bao nhiêu điểm cực tiểu?

Xem lời giải »

Câu 6:

Cho hàm số bậc bốn y = f(x) có đồ thị như hình bên dưới. Số điểm cực trị của hàm số $g (x) = f (- x^{3} + 3 x)$ là

Xem lời giải »

Câu 7:

Cho hàm số bậc năm y = f(x) liên tục trên $ℝ$ và có đồ thị hàm số $y = f^{'} (x)$ như trong hình bên. Tìm số điểm cực đại của hàm số $y = e^{f (x)} . π^{f^{3} (x)}$

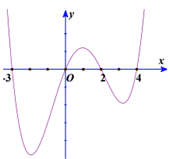
Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số y = f(x) có đúng ba điểm cực trị là x = -2, x = -1, x = 2 và có

Xem thêm bài tập Toán có lời giải hay khác: