Cho hàm số y = mx + 3. Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng d là lớn nhất.

Câu hỏi:

Trả lời:

Lời giải

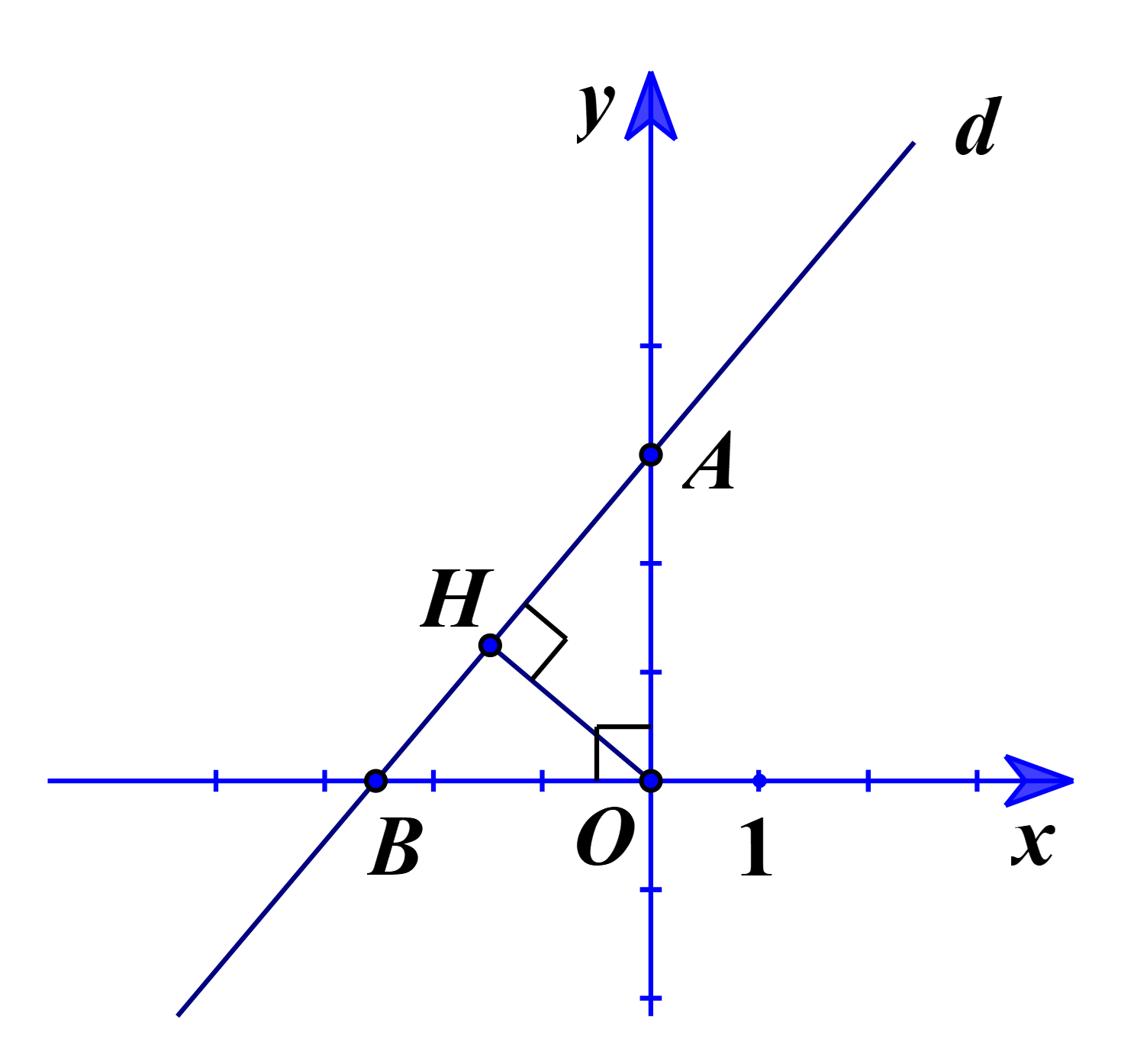
Gọi A, B lần lượt là giao điểm của đường thẳng d với các trục Oy, Ox.

Với x = 0, ta có: y = 3. Suy ra tọa độ A(0; 3).

Với y = 0, ta có: $x = \frac{{ - 3}}{m}$. Suy ra tọa độ $B\left( {\frac{{ - 3}}{m};0} \right)$.

Kẻ OH vuông góc với AB.

Khi đó khoảng cách từ gốc tọa độ O đến đường thẳng d là lớn nhất.

⇔ OH lớn nhất.

⇔ OH² lớn nhất.

Ta có OA = |3| = 3, $OB = \left| {\frac{{ - 3}}{m}} \right| = \frac{3}{{\left| m \right|}}$.

Tam giác OAB vuông tại O có OH là đường cao:

$\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{9} + \frac{{{m^2}}}{9} = \frac{{{m^2} + 1}}{9}$.

Suy ra $O{H^2} = \frac{9}{{{m^2} + 1}}$.

Ta có m² ≥ 0, ∀m.

⇔ m² + 1 ≥ 1, ∀m.

$\Leftrightarrow \frac{9}{{{m^2} + 1}} \le 9,\,\forall m$.

Dấu “=” xảy ra ⇔ m = 0.

Vậy m = 0 thỏa mãn yêu cầu bài toán.