Cho hàm số y=x3-3x2 Tìm tất cả các giá trị thực tham số m
Câu hỏi:
Cho hàm số .Tìm tất cả các giá trị thực tham số m để đường thẳng đi qua 2 điểm cực trị của đồ thị (C) tạo với đường thẳng một góc biết .
A. .
B.
C.
D. m = 2
Trả lời:
Chọn A
Đường thẳng đi qua ĐCĐ, ĐCT là
Đường thẳng đã cho có
Yêu cầu bài toán
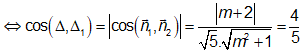
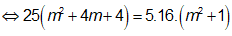
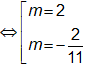
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
Xem lời giải »
Câu 2:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
Xem lời giải »
Câu 3:
Tìm các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C(0;-1) thẳng hàng
Xem lời giải »
Câu 4:
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: cắt đường tròn tâm bán kính bằng 1 tại 2 điểm mà diện tích tam giác lớn nhất
Xem lời giải »
Câu 5:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều
Xem lời giải »
Câu 6:
Tìm tất cả các giá trị thực của tham số m để điểm tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số một tam giác có diện tích nhỏ nhất
Xem lời giải »

