Cho hàm số y=f(x) xác định trên R \ {0}, liên tục trên mỗi khoảng xác định và có
Câu hỏi:
Cho hàm số y=f(x) xác định trên ℝ\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
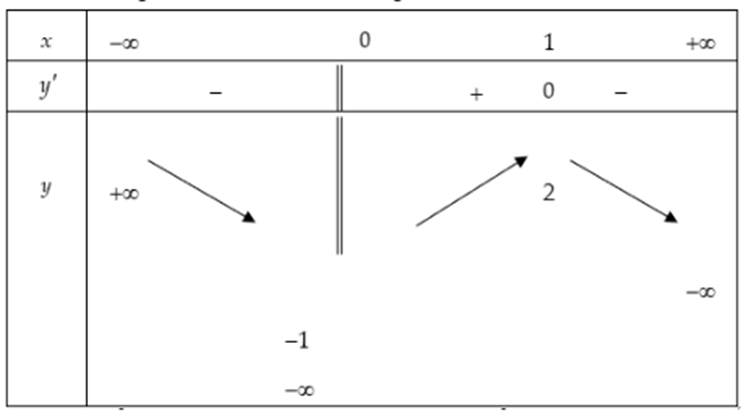
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm thực phân biệt.
Trả lời:
Dựa vào bảng biến thiên đã cho, phương trình f(x) = m có ba nghiệm phân biệt khi và chỉ khi −1 < m < 2 hay m ∈ (−1; 2) vì lúc đó, đường thẳng y = m cắt đồ thị hàm số y = f(x) tại ba điểm phân biệt.


