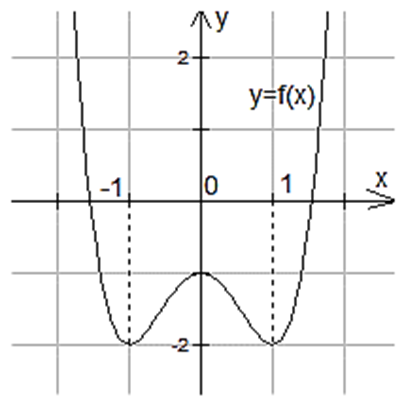
Cho hàm số y = f (x) có đồ thị đạo hàm y = f ′(x) như hình bên. Khẳng định nào sau đây là đúng? A. Hàm số y = f (x) − x2 − x đạt cực đại tại x = 0; B. Hàm số y = f (x) − x2 − x đạt cực
Câu hỏi:
Cho hàm số y = f (x) có đồ thị đạo hàm y = f ′(x) như hình bên.
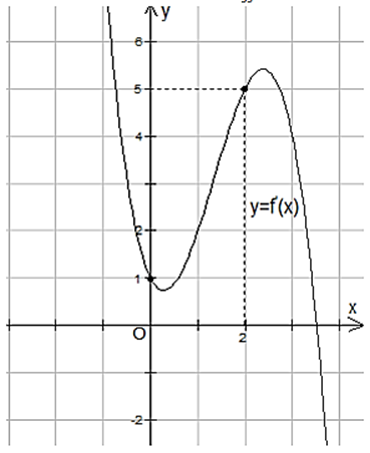
Khẳng định nào sau đây là đúng?
A. Hàm số y = f (x) − x2 − x đạt cực đại tại x = 0;
B. Hàm số y = f (x) − x2 − x đạt cực tiểu tại x = 0;
C. Hàm số y = f (x) − x2 − x không đạt cực trị tại x = 0;
D. Hàm số y = f (x) − x2 − x không có cực trị.
Trả lời:
Lời giải
Ta có: y′ = f ′(x) − (2x + 1)
y′ = 0 Û f ′(x) = (2x + 1)
Ta thấy đồ thị hàm số y = f ′(x) cắt y = 2x + 1 tại hai điểm x = 0 và x = 2 trên (−∞; 2)
Ta có bảng biến thiên trên (−∞; 2)
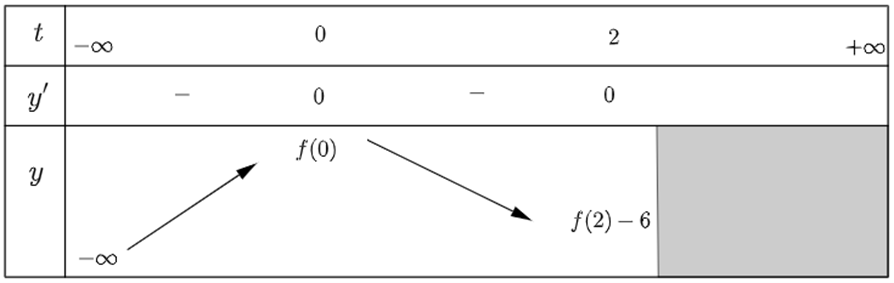
Từ bảng biến thiên hàm số đạt cực đại tại x = 0.
Chọn đáp án A.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho \(\left\{ \begin{array}{l}a + b \ne 0\\a;\;b \ne 0\end{array} \right.\). Chứng minh rằng: \[\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{{\left( {a + b} \right)}^2}}}} = \left| {\frac{1}{a} + \frac{1}{b} - \frac{1}{{a + b}}} \right|\].
Xem lời giải »
Câu 2:
Cho a, b, c là các số hữu tỉ khác 0 thỏa mãn a + b + c = 0. Chứng minh rằng: \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\) là bình phương của một số hữu tỉ.
Xem lời giải »
Câu 3:
Cho biểu thức: \[A = \sqrt {\frac{{{{\left( {{x^2} - 3} \right)}^2} + 12{x^2}}}{{{x^2}}}} + \sqrt {{{\left( {x + 2} \right)}^2} - 8x} \].
a) Rút gọn A.
b) Tìm các giá trị nguyên của x để giá trị của A là một số nguyên.
Xem lời giải »
Câu 4:
Cho biểu thức: \(P = \left( { - \frac{2}{3}{x^2}{y^3}{z^2}} \right){\left( { - \frac{1}{2}xy} \right)^3}{\left( {x{y^2}z} \right)^2}\).
a) Rút gọn biểu thức P.
b) Tìm bậc và hệ số biểu thức B.
c) Tìm giá trị các biến để P £ 0.
Xem lời giải »
Câu 5:
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị ở hình bên. Số nghiệm dương phân biệt của phương trình \(f\left( x \right) = - \sqrt 3 \) là:
Xem lời giải »
Câu 6:
Giải phương trình 2x2 + y2 − 6x + 2xy − 2y + 5 = 0.
Xem lời giải »
Câu 8:
Cho hai số hữu tỉ \(\frac{a}{b}\) và \(\frac{c}{d}\;\left( {b > 0,\;d > 0} \right)\). Chứng tỏ rằng:
a) Nếu \[\frac{a}{b} < \frac{c}{d}\] thì ad < bc.
b) Nếu ad < bc thì \[\frac{a}{b} < \frac{c}{d}\].
Xem lời giải »