Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Số nghiệm thực của phương trình f(2 + f(ex)) = 1 là: A. 1; B. 2; C. 4; D. 3.

Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ.

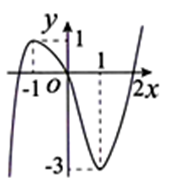Số nghiệm thực của phương trình f(2 + f(e^x)) = 1 là:

Lời giải

Đáp án đúng là: B

Số nghiệm của phương trình f(2 + f(e^x)) = 1 là số giao điểm của đồ thị hàm số y = f(2 + f(e^x)) và đường thẳng y = 1

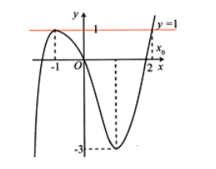
Dựa vào đồ thị hàm số ta có:

\(f\left( {2 + f\left( {{e^x}} \right)} \right) = 1\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2 + f\left( {{e^x}} \right) = - 1}\\{2 + f\left( {{e^x}} \right) = {x_0} \in (2;3)}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( {{e^x}} \right) = - 3}\\{f\left( {{e^x}} \right) = {x_0} - 2 \in (0;1)}\end{array}} \right.\)

TH1: f(e^x) = –3

\( \Leftrightarrow \left[ \begin{array}{l}{e^x} = 1\\{e^x} = {x_1} < - 1\end{array} \right. \Leftrightarrow x = 0\)

TH2: f(e^x) = x₀ – 2 ∈ (0; 1)

Suy ra phương trình có 3 nghiệm khác 0

Do đó: \(\left[ \begin{array}{l}{e^x} = a < 0\\{e^x} = b < 0\\{e^x} = c > 0\end{array} \right. \Leftrightarrow x = \ln c \ne 0\)

Vậy phương trình có 2 nghiệm phân biệt.