Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3 cm
Câu hỏi:
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3 cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích tam giác AMN.
A. 4 cm2;
B. 10 cm2;
C. 2 cm2;
D. 1 cm2.
Trả lời:
Đáp án đúng là: D.
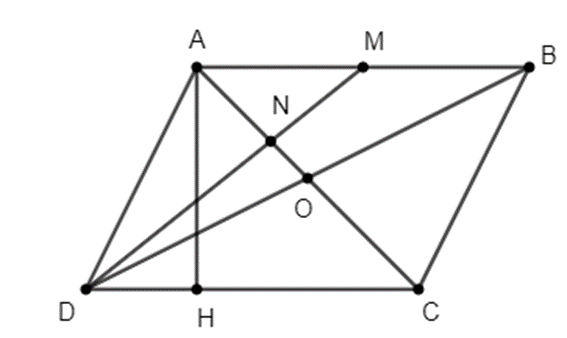
Tứ giác ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm O của mỗi đường.
Xét tam giác ABD ta có: AO và DM là hai đường trung tuyến của tam giác.
Mà AO ∩ DM = {N} nên N là trọng tâm tam giác ADB.
⇒ \(AN = \frac{2}{3}DM\) (tính chất đường trung tuyến của tam giác)
Suy ra \(NM = \frac{{DM}}{3}\)
+) Hai tam giác AMN và ADM có cùng đường cao hạ từ A nên:
\(\frac{{{S_{AMN}}}}{{{S_{ADM}}}} = \frac{{MN}}{{DM}} = \frac{1}{3}\)
\({S_{ADM}} = \frac{1}{2}AM.AH = \frac{1}{2}.\frac{4}{2}.3 = 3\) (cm2)
\( \Rightarrow {S_{AMN}} = \frac{1}{3}.{S_{ADM}} = \frac{1}{3}.3 = 1\) (cm2)

