Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA=a√6 vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 8πa2;
B. 2 πa2;
C. 2a2;
D. a2√2.
Trả lời:
Đáp án đúng là: A
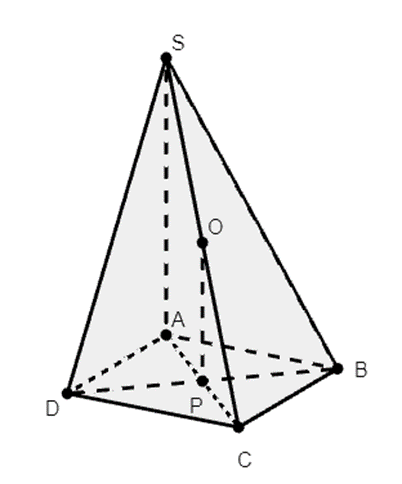
Tâm của mặt cầu là trung điểm O của đoạn thẳng SC.
Ta có: R = OA = OB = OC = OD = SO
= 12SC=12√SA2+AC2
=12√SA2+AB2+BC2=a√2
⇒ S = 4 πR2 = 8 πa2.
Câu 3:
Tìm m để phương trình cos2x + 2(m + 1)sinx − 2m – 1 = 0 có đúng 3 nghiệm x ∈ (0; π).
Câu 4:
Tìm m để phương trình 2sin2x – (2m + 1)sinx + 2m – 1 = 0 có nghiệm thuộc khoảng t ∈ (−1; 0).
Câu 5:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA = 2a, AB = a, BC=a√3. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Câu 6:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA = AC = 2a. Thể tích khối chóp S.ABC là
Câu 7:
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, cạnh AB = 3. Cạnh bên SA = 4 và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
Câu 8:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a và SA vuông góc với mặt phẳng (ABCD) và SA=a√2. Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng BM và SC bằng
