Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC
Câu hỏi:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA = 2a, AB = a, \(BC = a\sqrt 3 \). Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Trả lời:
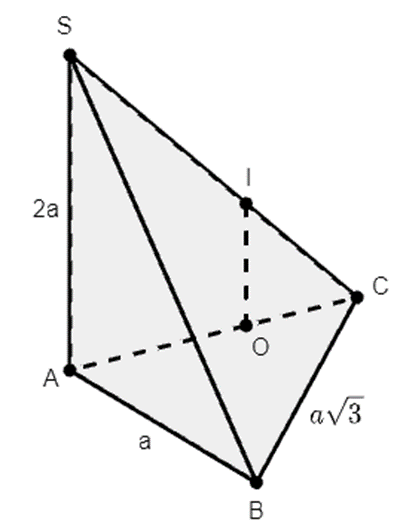
Gọi O, I lần lượt là trung điểm của AC và SC.
Khi đó OI là đường trung bình của tam giác SAC nên OI // SA.
Mà SA⊥(ABC) nên OI ⊥ (ABC).
Tam giác ABC vuông tại B nên O là tâm đường tròn ngoại tiếp tam giác ABC.
Mà OI ⊥ (ABC) nên OI chính là trục của (ABC) suy ra IA = IB = IC (1).
Lại có SA ⊥ (ABC) nên SA ⊥ AC.
Do đó tam giác SAC vuông tại A nên I chính là tâm đường tròn ngoại tiếp tam giác SAC, suy ra IS = IA = IC (2).
Từ (1) và (2) ta có IA = IB = IC = IS, hay I là tâm mặt cầu ngoại tiếp chóp S.ABC và bán kính mặt cầu là \(R = IS = \frac{1}{2}SC\).
Áp dụng định lý Py-ta-go trong tam giác vuông ABC, ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = 2a\).
Áp dụng định lí Py-ta-go trong tam giác vuông SAC, ta có:
\(SC = \sqrt {S{A^2} + A{C^2}} = 2a\sqrt 2 \)
Vậy \(R = \frac{1}{2}SC = a\sqrt 2 \).

