Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc (ABC) góc giữa
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng AC và SB.
Trả lời:
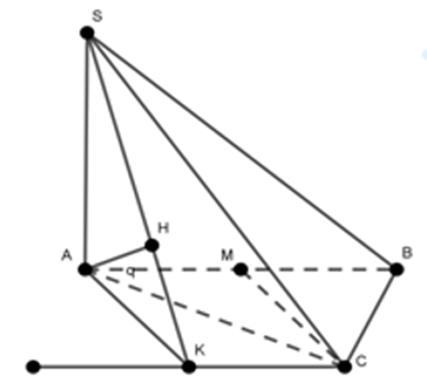
SA ⊥ (ABC) nên AB là hình chiếu của SB lên (ABC)
\[ \Rightarrow \widehat {(SB,(ABC))} = \widehat {(SB,AB)} = \widehat {SBA} = 60^\circ \]
\[ \Rightarrow SA = AB.\tan 60^\circ = a\sqrt 3 \]
Dựng d qua B và d // AC
Dựng AK ⊥ d tại K
Dựng AH ⊥ SK tại H
Ta có: BK ⊥ AK và BK ⊥ SA nên BK ⊥ (SAK)
Þ BK ⊥ AH
Mà SK ⊥ AH
Þ AH ⊥ (SBK)
Lại có: BK // AC; SK Ì (SBK); AC Ë (SBK)
Suy ra AC // (SBK)
Þ d(AC, SB) = d(A, (SBK)) = AH
Gọi M là trung điểm của AC suy ra BM ⊥ AC
Mà BK ⊥ AK và BK // AC nên AK ⊥ AC
Do đó AKBM là hình bình hành
\[ \Rightarrow AK = BM = \frac{{a\sqrt 3 }}{2}\]
Xét tam giác SAK vuông tại A ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{A{K^2}}} + \frac{1}{{S{A^2}}} = \frac{5}{{3{a^2}}}\]
\[AH = \frac{{a\sqrt {15} }}{5}\]
Vậy \[d(AC,SB) = \frac{{a\sqrt {15} }}{5}\].