Tìm tập xác định D của hàm số y = log2(x^3 - 8)1000

Chứng minh trên đường tròn lượng giác gốc A, cung lượng giác $\frac{{k2\pi }}{3}$ có các điểm biểu diễn tạo thành tam giác đều.

Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ dưới đây. Tìm số nghiệm của phương trình f(x) = 3. 

Chứng minh hai góc kề nhau của một hình bình hành không thể có số đo là 40° và 50°.

Tìm chu kì của hàm số $y = \sin \sqrt x$.

Cho hàm số y=f(x) xác định trên ℝ\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

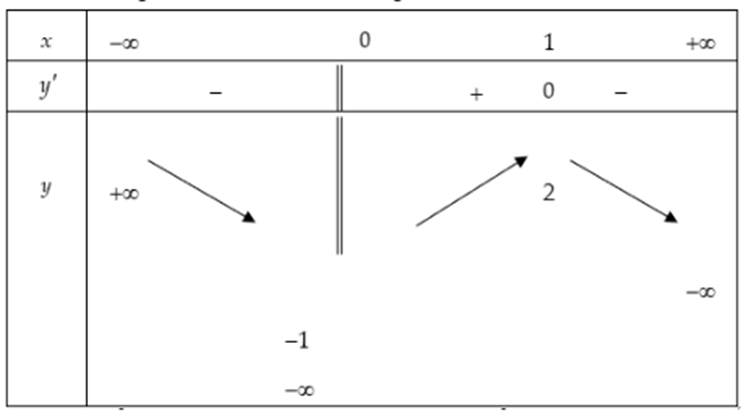
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm thực phân biệt.

Tìm số điểm biểu diễn các nghiệm của phương trình $\sin \left( {2x + \frac{\pi }{3}} \right) = \frac{1}{2}$trên đường tròn lượng giác.

Cho hàm số $y = \frac{{mx - 2m - 3}}{{x - m}}$   với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng (2; +∞). Tìm số phần tử của S.

Tìm tất cả các giá trị của tham số m để hàm số $y = {\log _{2020}}(mx - m + 2)$xác định trên $[1; + \infty )$.