Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết \(\frac{{{V_{S.AHB}}}}{{{V_{S.ACB}}}} = \frac{{16}}{{19}}\). Tính Thể tích của khối chóp S.ABC.
Trả lời:
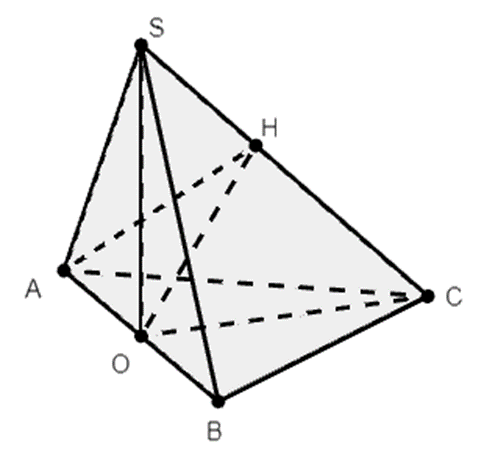
Gọi O là trung điểm của AB ⇒ SO ⊥ (ABC)
Ta có: SC ⊥ AH; SC ⊥ AB
Suy ra SC ⊥ (AHB) ⇒ SC ⊥ OH
Trong ∆SOC vuông tại O có:
SH.SC = SO2 \( \Rightarrow \frac{{SH}}{{SC}} = \frac{{S{O^2}}}{{S{C^2}}}\)
Ta có: \(\frac{{{V_{S.AHB}}}}{{{V_{S.ACB}}}} = \frac{{16}}{{19}}\)
\( \Leftrightarrow \frac{{SH}}{{SC}} = \frac{{16}}{{19}} \Leftrightarrow \frac{{S{O^2}}}{{S{C^2}}} = \frac{{16}}{{19}}\)
\( \Leftrightarrow \frac{{S{O^2}}}{{S{O^2} + \frac{3}{4}}} = \frac{{16}}{{19}} \Rightarrow SO = 2\)
Vậy \[V = \frac{1}{3}\,.\,{S_{ABC}}\,.\,SO = \frac{1}{3}\,.\,2\,.\,\frac{{\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{6}\].