Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 điểm A1; B1; C1
Câu hỏi:
Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 điểm A1; B1; C1; D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích, … , S100 (tham khảo hình bên). Tính tổng S = S1 + S2 + S3 + … + S100.
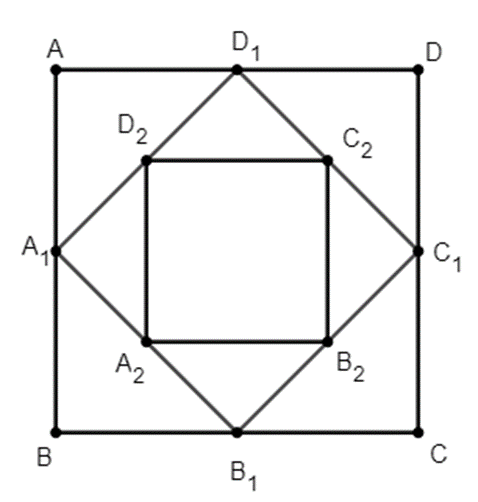
Trả lời:
Ta có: S1 = a2; \({S_2} = \frac{1}{2}{a^2};{S_3} = \frac{1}{4}{a^2}\); …
Do đó S1; S2; S3; …; S100 là cấp số nhân với số hạng đầu u1 = S1 = a2 và công bội \(q = \frac{1}{2}\).
Suy ra S = S1 + S2 + S3 + … + S100 = \({S_1}.\frac{{1 - {q^n}}}{{1 - q}} = \frac{{{a^2}\left( {{2^{100}} - 1} \right)}}{{{2^{99}}}}\).

