Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB và SC. Thể tích của khối cầu ngoại tiếp hình chóp A.HKCB bằng:
A. \(\sqrt 2 \pi {a^3}\)
B. \(\frac{{\sqrt 2 \pi {a^3}}}{3}\)
C. \(\frac{{\pi {a^3}}}{6}\)
D. \(\frac{{\pi {a^3}}}{2}\).
Trả lời:
Đáp án đúng là: B
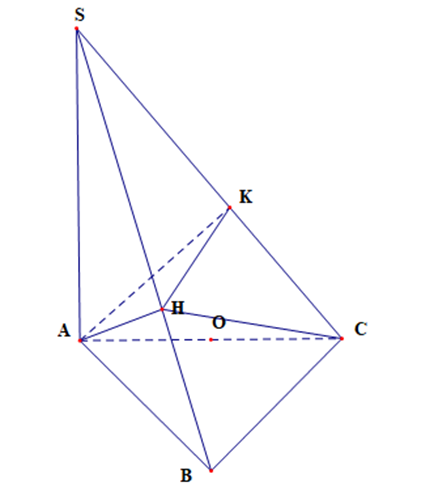
Gọi O là trung điểm của AC
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot SA}\\{BC \bot AB}\end{array} \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH} \right.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AH \bot SB}\\{AH \bot BC}\end{array} \Rightarrow AH \bot (SBC) \Rightarrow AH \bot HC} \right.\)
Suy ra tam giác AHC vuông tại H
Do đó H thuộc mặt cầu tâm \({\rm{O}}\) đường kính AC
Vì tam giác AKC vuông tại K nên K thuộc mặt cầu tâm \({\rm{O}}\) đường kính AC
Vì tam giác ABC vuông tại B nên B thuộc mặt cầu tâm \({\rm{O}}\) đường kính AC
Suy ra 5 điềm A, H, K, B, C đều thuộc mặt cầu tâm O đường kính AC hay khối chóp A.HKCB nội tiếp mặt cầu tâm O đường kính AC
Khi đó bán kính mặt cầu là: \(R = \frac{{AC}}{2}\)
Tam giác \({\rm{ABC}}\) vuông cân tại B và BC = a \( \Rightarrow AC = a\sqrt 2 \Rightarrow R = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Suy ra thể tích của khối cầu ngoại tiếp hình chóp A.HKCB là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {\left( {\frac{{a\sqrt 2 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 2 }}{3}\)
Vậy ta chọn đáp án B.


