Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a, biết
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a, biết SA ⊥ (ABC) và SB với đáy một góc 60. Thể tích khối chóp S.ABC là
A. V=a3√624;
B. V=a3√324;
C. V=a3√68;
D. V=a3√648.
Trả lời:
Đáp án đúng là: A.
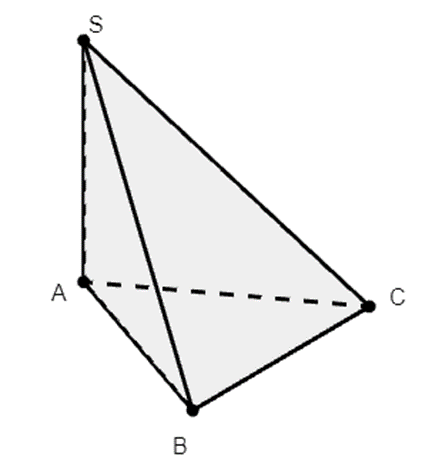
Vì SA vuông góc với (ABC)
⇒ A là hình chiếu của S trên (ABC)
⇒ AB là hình chiếu của SB trên (ABC)
⇒ (SB, (ABC)) = (SB, AB) =^SBA=60∘
Tam giác vuông cân ABC tại B
⇒ AB=BC=AC.sin45∘=AC.√22=a√22
Tam giác SAB vuông tại A
⇒SA=AB.tan^SBA=a√22.tan60∘=a√62
Thể tích khối chóp S.ABC là:
V=13.SABC.SA=13.(12.a√22.a√22).a√62=a3√624.
