Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a. Tam giác SAB
Câu hỏi:
A. \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 2 }}{2}.\)
B. \({S_{\Delta ABC}} = {a^2}\sqrt 2 .\)
C.\({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 2 }}{4}.\)
D. \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 2 }}{6}.\)
Trả lời:
Đáp án đúng là: A
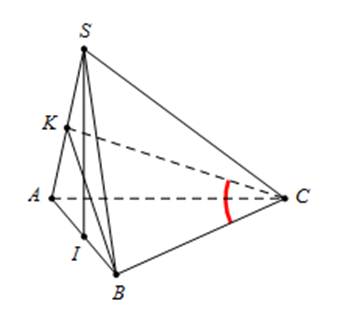
Gọi I là trung điểm của AB, tam giác SAB đều \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{SI = \frac{{a\sqrt 3 }}{2}}\\{SI \bot AB}\end{array}} \right.\)
Mà \(\left( {SAB} \right) \bot \left( {ABC} \right) \Rightarrow SI \bot \left( {ABC} \right);\left\{ {\begin{array}{*{20}{l}}{SI \bot AC}\\{AB \bot AC}\end{array} \Rightarrow AC \bot \left( {SAB} \right)} \right.\).
Kẻ BK vuông góc với SA tại K, vì AC ⊥ (SAB) nên \(AC \bot BK \Rightarrow BK \bot (S\) và \(BK = \frac{{a\sqrt 3 }}{2}\)
Do đó, góc giữa BC và (SAC) là \(\widehat {BCK} \Rightarrow \widehat {BCK} = 30^\circ .\)
Khi đó \(BC = \frac{{BK}}{{{\rm{sin}}\widehat {BCK}}} = a\sqrt 3 \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} = a\sqrt 2 \).
Vậy diện tích tam giác ABC là \({S_{\Delta ABC}} = \frac{1}{2} \cdot AB \cdot AC = \frac{{{a^2}\sqrt 2 }}{2}\).
Đáp án cần chọn là: \({\rm{A}}\)

