Giá trị nhỏ nhất Fmin của biểu thức F(x; y) = y - x trên miền xác định y - 2x < = 2
Câu hỏi:
Giá trị nhỏ nhất Fmin của biểu thức F(x; y) = y − x trên miền xác định
\[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\] là
A. Fmin = 1 khi x = 2, y = 3.
B. Fmin = 2 khi x = 0, y = 2.
C. Fmin = 3 khi x = 1, y = 4.
D. Fmin = 4 khi x = 0, y = 0.
Trả lời:
Đáp án đúng là: A
Biểu diễn miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\] trên hệ trục tọa độ như hình dưới đây
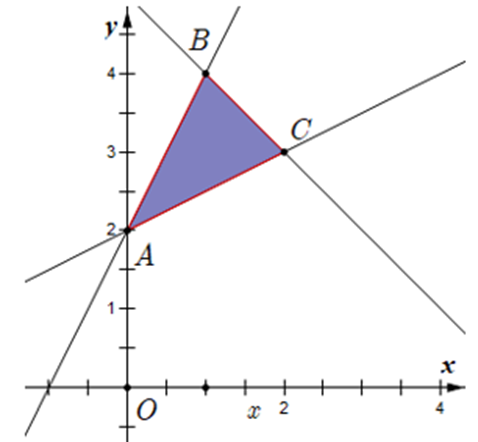
Nhận thấy biết thức F = y − x chỉ đạt giá trị nhỏ nhất tại các điểm A, B hoặc C.
Ta có:
Tại A(0; 2) thì F = 2.
Tại B(1; 4) thì F = 3.
Tại A(2; 3) thì F = 1.
Vậy Fmin = 1 khi x = 2, y = 3.
Đáp án cần chọn là: A.

