Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, BC và P là điểm
Câu hỏi:
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, BC và P là điểm nằm trên cạnh AB sao cho \(AP = \frac{1}{3}AB.\) Gọi Q là giao điểm của SC và (MNP). Tính tỉ số \(\frac{{SQ}}{{SC}}.\)
Trả lời:
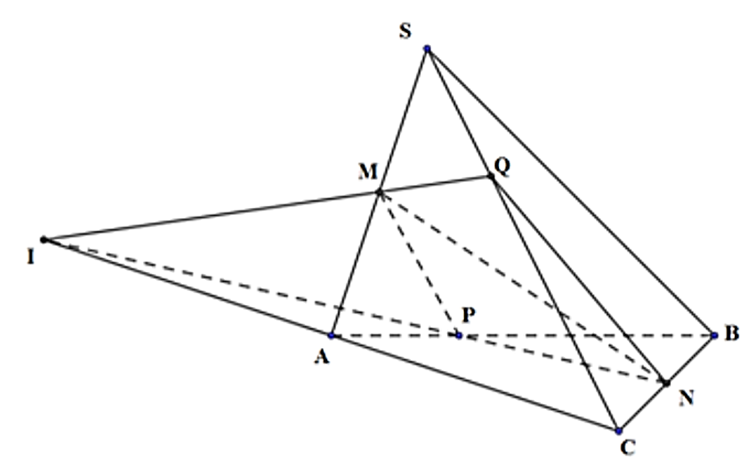
Do \(\frac{{AP}}{{AB}} = \frac{1}{3},\) \(\frac{{CN}}{{CB}} = \frac{1}{2}\) ⇒ NP không song song với AC.
Trong (ABC), gọi I = NP ∩ AC.
Trong (SAC), gọi M = IQ ∩ SA.
Do \(IM \subset \left( {MNP} \right)\) ⇒ Q = SC ∩ (MNP).
· Xét ∆IBC:
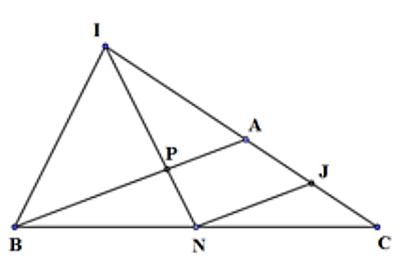
Kẻ NJ song song AB (J ∈ IC).
Do N là trung điểm của BC ⇒ J là trung điểm của AC ⇒ AC = 2AJ.
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{AP\parallel NJ}\\{\frac{{IP}}{{NP}} = 2}\end{array}} \right.\) ⇒ \(\frac{{IA}}{{AJ}} = 2\) ⇒ AI = 2AJ ⇒ IA = AC = (2AJ)
⇒ A là trung điểm của IC.
· Xét ∆SIC:

Kẻ AK song song IQ (K ∈ SC).
Do A là trung điểm của IC ⇒ K là trung điểm của QC
⇒ QK = KC
Ta có: MQ // AK, M là trung điểm của SA ⇒ Q là trung điểm của SK
⇒ SQ = QK ⇒ SQ = QK = KC ⇒ \(SQ = \frac{1}{3}SC\) ⇒ \(\frac{{SQ}}{{SC}} = \frac{1}{3}.\)

