Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt bên SAB là tam giác
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt bên SAB là tam giác đều cạnh \[\sqrt 3 a\],ABC là tam giác vuông tại A có cạnh AC = a, góc giữa AD và (SAB) bằng 30°. Thể tích khối chóp S.ABCD bằng:
A. \({a^3}\)
B. \(\frac{{\sqrt 3 {a^3}}}{6}\)
C. \(\frac{{\sqrt 3 {a^3}}}{2}\)
D. \(\frac{{\sqrt 3 {a^3}}}{4}\)
Trả lời:
Đáp án đúng là: C
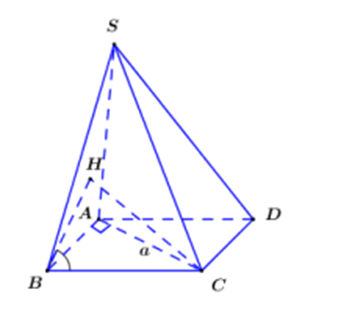
Vì BC // AD\({\rm{\;}} \Rightarrow \angle \left( {AD;\left( {SAB} \right)} \right) = \angle \left( {BC;\left( {SAB} \right)} \right){\rm{.\;}}\)
Gọi H là hình chiếu vuông góc của C lên (SAB) ⇒ BH là hình chiếu của BC lên (SAB)
\( \Rightarrow \angle \left( {BC;\left( {SAB} \right)} \right) = \angle \left( {BC;BH} \right) = \angle HBC = 30^\circ \)
Xét tam giác vuông \({\rm{ABC}}\) có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {3{a^2} + {a^2}} = 2a\)
Xét tam giác vuông \({\rm{BCH}}\) có \(CH = BC \cdot {\rm{sin}}30^\circ = 2a \cdot \frac{1}{2} = a\).
Vì ∆SAB đều cạnh \(a\sqrt 3 \) nên \({S_{\Delta SAB}} = \frac{{{{(a\sqrt 3 )}^2} \cdot \sqrt 3 }}{4} = \frac{{3\sqrt 3 {a^2}}}{4}\).
\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}CH \cdot {S_{\Delta SAB}} = \frac{1}{{\sqrt 3 }} \cdot a \cdot \frac{{3\sqrt 3 {a^2}}}{4} = \frac{{\sqrt 3 {a^3}}}{4}.\)
Vậy \({V_{S.ABCD}} = 2{V_{S.ABC}} = \frac{{\sqrt 3 {a^3}}}{2}\).

