Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD, OC.
a) Tìm Tìm giao tuyến của mặt phẳng (MNP) với mp (SAC).
b) Tìm giao điểm của SA với mp (MNP).
c) Tìm thiết diện của S.ABCD với (AMN).
Trả lời:
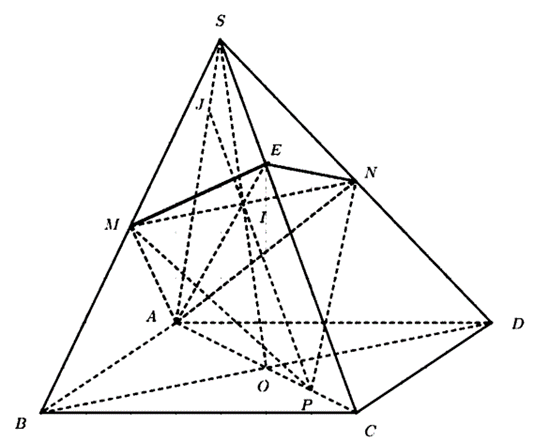
a) P ∈ (MNP) ∩ (SAC)
SO và MN ⊂ (SBD) ⇒ SO cắt được MN
Gọi MN ∩ SO = I
⇒ I ∈ (MNP) ∩ (SAC)
⇒ (MNP) ∩ (SAC) = PI
b) Gán SA ⊂ (SAC)
Mà (SAC) ∩ (MNP) = PI
⇒ SA ∩ (MNP) = SA ∩ PI = J
c) AI, SC ⊂ (SAC) ⇒ AI cắt được SC
Gọi AI ∩ SC = E
⇒(AMN) ∩ (SAB) = AM
(AMN) ∩ (SBC) = ME
(AMN) ∩ (SCD) = EN
(AMN) ∩ (SAD) = AN
⇒ Thiết diện là tứ diện AMEN.

