Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là một
Câu hỏi:
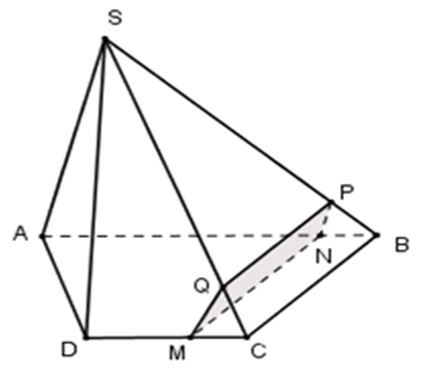
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là một điểm trên cạnh CD; (α) là mặt phẳng qua M và song song với SA và BC. Thiết diện của mp(α) với hình chóp là:
A. Hình tam giác.
B. Hình thang.
C. Hình bình hành.
D. Hình chữ nhật.
Trả lời:
Đáp án đúng là: B
\(\left\{ {\begin{array}{*{20}{c}}{{\rm{M}} \in \left( \alpha \right) \cap \left( {{\rm{ABCD}}} \right)}\\{{\rm{BC//}}\left( \alpha \right)}\\{{\rm{BC}} \subset \left( {{\rm{ABCD}}} \right)}\end{array}} \right.\)
⇒ (α) ∩ (ABCD) = MN // BC
N ∈ AB (1)
Tương tự \(\left\{ {\begin{array}{*{20}{c}}{{\rm{N}} \in \left( \alpha \right) \cap \left( {{\rm{SAB}}} \right)}\\{{\rm{SA//}}\left( \alpha \right)}\\{{\rm{SA}} \subset \left( {{\rm{SAB}}} \right)}\end{array}} \right.\)
⇒ (α) ∩ (SAB) = NP // SA
P ∈ SB \(\left\{ {\begin{array}{*{20}{c}}{{\rm{P}} \in \left( \alpha \right) \cap \left( {{\rm{SBC}}} \right)}\\{{\rm{BC//}}\left( \alpha \right)}\\{{\rm{BC}} \subset \left( {{\rm{SBC}}} \right)}\end{array}} \right.\)
⇒ (α) ∩ (SBC) = PQ // BC
Q ∈ SC (2)
Từ (1) và (2) suy ra MN // PQ.
Vậy thiết diện là hình thang MNPQ.
Đáp án cần chọn là: B.

