Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng của D qua C. Tính vecto AE
Câu hỏi:
Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng của D qua C. Tính \[\overrightarrow {AE} \cdot \overrightarrow {AB} \]
A. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = 2{a^2}.\]
B. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = \sqrt 3 {a^2}.\]
C. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = \sqrt 5 {a^2}.\]
D. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = 5{a^2}.\]
Trả lời:
Đáp án đúng là: A
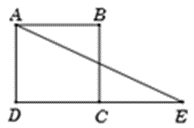
Ta có C là trung điểm của DE nên DE = 2a
Khi đó
\[\overrightarrow {AE} \cdot \overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right) \cdot \overrightarrow {AB} .\]
\[ = \underbrace {\overrightarrow {AD} \cdot \overrightarrow {AB} }_0 + \overrightarrow {DE} \cdot \overrightarrow {AB} \]
\[ = DE \cdot AB \cdot cos\left( {\overrightarrow {DE} ,\overrightarrow {AB} } \right)\]
= DE.AB.cos0° = 2a2

