Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD = 60 độ
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc \(\widehat {BAD} = 60^\circ \); \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi a là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đây đúng?
A. \(\tan a = \sqrt 5 \);
B. \(\tan a = \frac{{\sqrt 5 }}{5}\);
C. \(\tan a = \frac{{\sqrt 3 }}{2}\);
Trả lời:
Đáp án đúng là: A
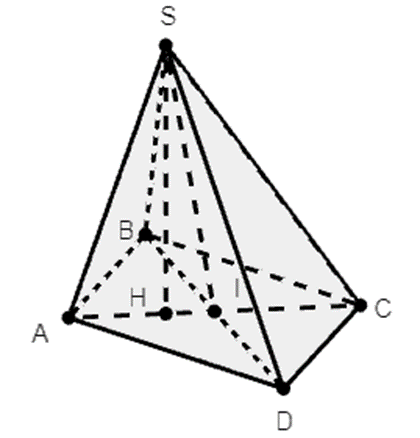
Từ giả thiết suay ra tam giác ABD đều cạnh a.
Gọi H là hình chiếu của S trên mặt phẳng (ABCD).
Do SA = SB = SC nên suy ra H cách đều các đỉnh của tam giác ABD hay H là tâm của tam giác đều ABD.
Suy ra \(HI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{6}\) và \(SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{6}\)
Vì ABCD là hình thoi nên HI ⊥ BD
Tam giác SBD cân tại S nên SI ⊥ BD
Do đó \(\widehat {\left( {\left( {SBD} \right),\,\,\left( {ABCD} \right)} \right)} = \widehat {\left( {SI,\,\,AI} \right)} = \widehat {SIH}\)
Trong tam giác vuông SHI, có \(\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \sqrt 5 \).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
Xem lời giải »
Câu 2:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
Xem lời giải »
Câu 3:
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và \(\widehat {ABC} = 120^\circ \). Các cạnh AA', A'B, A'D cùng tạo với đáy một góc 60°. Tính theo a thể tích V của khối lăng trụ đã cho.
Xem lời giải »
Câu 4:
Quãng đường AB gồm một đoạn lên dốc dài 4 km và một đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
Xem lời giải »
Câu 5:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
Xem lời giải »
Câu 6:
Chứng minh rằng với mọi số nguyên dương n ta luôn có n3 + 5n chia hết cho 6.
Xem lời giải »
Câu 7:
Cho x là số thực dương, số hạng không chứa x trong khai triển nhị thức \({\left( {x + \frac{2}{{\sqrt x }}} \right)^{30}}\) là:
Xem lời giải »
Câu 8:
Giá trị lớn nhất của hàm số y = x4 – 4x2 + 9 trên đoạn [−2; 3] bằng:
Xem lời giải »


